पूर्व दर्शन:

मास्को क्षेत्र के शिक्षा मंत्रालय

जीओयू एनपीओ वोकेशनल स्कूल नंबर 37

परियोजना:

क्वाड्रेटिव समीकरणों और पैरामीटर्स के साथ असमानताओं का»

प्रदर्शन किया -

मात्सुक गैलिना निकोलायेवना,

गणित शिक्षक, एन.पी.ओ

व्यावसायिक स्कूल नंबर 37 एमओ।

जी। नोगिंस्क, 2011

1 परिचय

4. प्रारंभिक परिस्थितियों में द्विघात समीकरणों को हल करने की तकनीक।

6. सामान्य रूप में मापदंडों के साथ द्विघात असमानताओं को हल करने की तकनीक।

7. प्रारंभिक परिस्थितियों में द्विघात असमानताओं को हल करने की विधि।

8. निष्कर्ष।

9. साहित्य।

1. परिचय।

एक व्यावसायिक स्कूल में गणित पढ़ाने का मुख्य कार्य गणितीय ज्ञान और दैनिक जीवन और काम में छात्रों के लिए आवश्यक कौशल की एक मजबूत और जागरूक महारत सुनिश्चित करना है, जो संबंधित विषयों का अध्ययन करने और शिक्षा जारी रखने के साथ-साथ व्यावसायिक गतिविधियों में भी पर्याप्त है। जिसके लिए पर्याप्त उच्च गणितीय संस्कृति की आवश्यकता होती है।

मेटल वर्किंग, इलेक्ट्रिकल वर्क और वुडवर्किंग में व्यवसायों से संबंधित व्यावहारिक समस्याओं के समाधान के माध्यम से गणित का प्रोफाइल शिक्षण किया जाता है। आधुनिक समाज में जीवन के लिए, संचार की एक गणितीय शैली बनाना महत्वपूर्ण है, जो कुछ मानसिक कौशलों में प्रकट होती है। मापदंडों वाले कार्यों में नैदानिक ​​​​और भविष्यसूचक मूल्य होते हैं। उनकी मदद से, आप प्रारंभिक गणित के मुख्य वर्गों के ज्ञान, तार्किक सोच के स्तर, शोध कार्य के प्रारंभिक कौशल की जांच कर सकते हैं।

मापदंडों के साथ शिक्षण कार्यों के लिए छात्रों से महान मानसिक और अस्थिर प्रयासों, विकसित ध्यान और गतिविधि, रचनात्मक पहल और सामूहिक संज्ञानात्मक कार्य जैसे गुणों के विकास की आवश्यकता होती है। मापदंडों के साथ कार्य अंतिम राज्य प्रमाणन की तैयारी में दूसरे वर्ष में एक सामान्यीकरण पुनरावृत्ति के दौरान और तीसरे वर्ष में अतिरिक्त कक्षाओं में उन छात्रों की तैयारी के लिए उन्मुख होते हैं जिन्होंने अंतिम परीक्षा के रूप में लेने की इच्छा व्यक्त की है। एकीकृत राज्य परीक्षा।

गणितीय शिक्षा के आधुनिकीकरण की मुख्य दिशा एकीकृत राज्य परीक्षा की शुरूआत के माध्यम से अंतिम प्रमाणन के तंत्र का विकास है। गणित के कार्यों में, पैरामीटर वाले कार्यों को हाल के वर्षों में पेश किया गया है। विश्वविद्यालयों में प्रवेश परीक्षा के लिए ऐसे कार्य अनिवार्य हैं। ऐसे कार्यों की उपस्थिति बहुत महत्वपूर्ण है, क्योंकि उनका उपयोग प्रारंभिक गणित के सूत्रों में महारत हासिल करने की तकनीक, समीकरणों और असमानताओं को हल करने के तरीकों, तर्क की तार्किक श्रृंखला बनाने की क्षमता, आवेदक की तार्किक सोच के स्तर की जांच करने के लिए किया जाता है। . पिछले कुछ वर्षों में यूएसई के पिछले परिणामों के विश्लेषण से पता चलता है कि स्नातक ऐसे कार्यों को बड़ी कठिनाई से हल करते हैं, और कई उन्हें शुरू भी नहीं करते हैं। अधिकांश या तो ऐसे कार्यों का सामना नहीं करते हैं, या बोझिल गणनाएँ करते हैं। इसका कारण स्कूली पाठ्यपुस्तकों में इस विषय पर कार्यों की प्रणाली का अभाव है। इस संबंध में, व्यावसायिक अभिविन्यास से संबंधित मापदंडों और लागू समस्याओं के साथ समस्याओं को हल करने पर परीक्षा की तैयारी में स्नातक समूहों में विशेष विषयों का संचालन करना आवश्यक हो गया।

इन विषयों का अध्ययन तीसरे वर्ष के छात्रों के लिए है जो बीजगणित में जटिलता के बढ़े हुए स्तर और विश्लेषण की शुरुआत की समस्याओं को हल करना सीखना चाहते हैं। ऐसी समस्याओं का समाधान उनके लिए काफी मुश्किलें पैदा करता है। यह इस तथ्य के कारण है कि पैरामीटर के साथ प्रत्येक समीकरण या असमानता साधारण समीकरणों और असमानताओं का एक पूरा वर्ग है, जिनमें से प्रत्येक के लिए एक समाधान प्राप्त किया जाना चाहिए।

मापदंडों के साथ समस्याओं को हल करने की प्रक्रिया में, मानव सोच की तकनीकों और तरीकों के शस्त्रागार में स्वाभाविक रूप से प्रेरण और कटौती, सामान्यीकरण और संक्षिप्तीकरण, विश्लेषण, वर्गीकरण और व्यवस्थितकरण और सादृश्य शामिल हैं। चूंकि व्यावसायिक स्कूलों में पाठ्यक्रम गणित में परामर्श प्रदान करता है, जो प्रशिक्षण सत्रों की अनुसूची में उपलब्ध हैं, यह उन छात्रों के लिए उचित है जिनके पास पर्याप्त गणितीय प्रशिक्षण है, जो अध्ययन किए जा रहे विषय में रुचि रखते हैं, एक विश्वविद्यालय में प्रवेश के आगे के लक्ष्य के साथ , ओलंपियाड, गणितीय प्रतियोगिताओं, विभिन्न प्रकार की परीक्षाओं, विशेष रूप से यूएसई की तैयारी के लिए मापदंडों के साथ समस्याओं को हल करने के लिए इन घंटों का उपयोग करना। विशेष रूप से महत्वपूर्ण व्यावहारिक और व्यावहारिक प्रकृति की ऐसी समस्याओं का समाधान है, जो विभिन्न अध्ययनों को करने में मदद करेगा।

2. लक्ष्य, मुख्य कार्य, विधियाँ, प्रौद्योगिकियाँ, ज्ञान की आवश्यकताएँ।

परियोजना के लक्ष्य:

• द्विघात समीकरणों और असमानताओं के अध्ययन के लिए कम किए गए मापदंडों के साथ समस्याओं को हल करने के लिए कौशल और क्षमताओं का गठन।
• विषय में रुचि का निर्माण, गणितीय क्षमताओं का विकास, परीक्षा की तैयारी।
• समीकरणों और असमानताओं को हल करने की तकनीकों और विधियों के बारे में गणितीय विचारों का विस्तार।
• तार्किक सोच और अनुसंधान कौशल का विकास।
• रचनात्मक, अनुसंधान और संज्ञानात्मक गतिविधियों का परिचय।
• स्वतंत्र रचनात्मक कार्य के लिए शर्तें प्रदान करना।
• मानसिक और अस्थिर प्रयासों के छात्रों में शिक्षा, विकसित ध्यान, गतिविधि, रचनात्मक पहल, सामूहिक संज्ञानात्मक कार्य के कौशल।

परियोजना के मुख्य कार्य:

• छात्रों को गणित में उनकी रुचि और इसके विकास के लिए व्यक्तिगत अवसरों का एहसास करने का अवसर प्रदान करें।
• तथ्यात्मक ज्ञान और कौशल को आत्मसात करने में योगदान दें।
• अनुप्रयुक्त अनुसंधान के क्षेत्र में मापदंडों के साथ कार्यों का व्यावहारिक महत्व दिखाएं।
• मानक और गैर-मानक समीकरणों और असमानताओं को हल करना सिखाना।
• गणित में ज्ञान को गहरा करने के लिए, विषय में एक सतत रुचि के गठन के लिए प्रदान करना।
• छात्रों की गणितीय क्षमताओं की पहचान करना और उनका विकास करना।
• विश्वविद्यालयों में प्रवेश के लिए तैयारी प्रदान करें।
• उच्च गणितीय संस्कृति की आवश्यकता वाली व्यावसायिक गतिविधियों के लिए प्रशिक्षण प्रदान करें।
• बौद्धिक और संवादात्मक गुणों के विकास में योगदान देने वाले अनुसंधान और परियोजना गतिविधियों को व्यवस्थित करें।

कक्षाओं के संचालन में उपयोग की जाने वाली विधियाँ:

• व्याख्यान - छात्रों के साथ बातचीत के साथ सैद्धांतिक सामग्री के हस्तांतरण के लिए।
• सेमिनार - सिद्धांत की चर्चा पर सामग्री को समेकित करने के लिए।
• कार्यशाला - गणितीय समस्याओं को हल करने के लिए।
• चर्चाएँ - उनके निर्णयों के विकल्पों पर बहस करना।
• समूह और व्यक्तिगत गतिविधि के विभिन्न रूप।
• अनुसंधान गतिविधि, जिसके माध्यम से आयोजित किया जाता है: उपचारात्मक सामग्री के साथ काम करना, संदेशों की तैयारी, सार की रक्षा और रचनात्मक कार्य।
• व्याख्यान एक कंप्यूटर और एक प्रोजेक्टर का उपयोग कर प्रस्तुतीकरण हैं।

प्रयुक्त प्रौद्योगिकियां:

• शिक्षा की व्याख्यान और संगोष्ठी प्रणाली।
• सूचना एवं संचार प्रोद्योगिकी।
• मानसिक क्षमताओं को विकसित करने के उद्देश्य से शिक्षण में एक शोध पद्धति।
• समस्या आधारित अधिगम, जो समस्या को प्रस्तुत कर, समस्या के विभिन्न विकल्पों पर चर्चा कर अनुसंधान के लिए प्रेरणा प्रदान करता है।
• गतिविधि पद्धति की तकनीक, जो छात्रों के संज्ञानात्मक हितों को सामने लाने में मदद करती है।

छात्रों के ज्ञान के लिए आवश्यकताएँ।

द्विघात समीकरणों और असमानताओं को मापदंडों के साथ हल करने के विभिन्न तरीकों का अध्ययन करने के परिणामस्वरूप, छात्रों को कौशल हासिल करना चाहिए:

• द्विघात समीकरण और द्विघात असमानता में पैरामीटर की अवधारणा को दृढ़ता से मास्टर करने के लिए;
• मापदंडों के साथ द्विघात समीकरणों को हल करने में सक्षम हों।
• मापदंडों के साथ द्विघात असमानताओं को हल करने में सक्षम हो।
• द्विघात फलन के मूल ज्ञात कीजिए।
• द्विघात कार्यों के रेखांकन बनाएँ।
• एक द्विघात त्रिपद का अन्वेषण करें।
• समान परिवर्तनों के तर्कसंगत तरीकों को लागू करें।
• सबसे अधिक इस्तेमाल किए जाने वाले ह्यूरिस्टिक्स का उपयोग करें।
• व्यक्तिगत कंप्यूटर पर काम करते समय अधिग्रहीत ज्ञान को लागू करने में सक्षम हों।

नियंत्रण के रूप।

• सबक - स्व-मूल्यांकन और साथियों का मूल्यांकन।
• शैक्षिक परियोजनाओं की प्रस्तुति।
• परिक्षण।
• रेटिंग - टेबल।
• पिछले वर्षों की परीक्षाओं के संग्रह से होमवर्क असाइनमेंट।
• टेस्ट पेपर्स।

3. सामान्य रूप में मापदंडों के साथ द्विघात समीकरणों को हल करने की तकनीक।

मापदंडों वाले कार्यों से डरो मत। सबसे पहले, समीकरणों और असमानताओं को मापदंडों के साथ हल करते समय, आपको वह करने की ज़रूरत है जो किसी भी समीकरण और असमानता को हल करते समय किया जाता है - दिए गए समीकरणों या असमानताओं को एक सरल रूप में लाएं, यदि संभव हो तो: तर्कसंगत अभिव्यक्ति को कारक बनाएं, कम करें, कारक लें कोष्ठक से बाहर, आदि। डी। ऐसे कार्य हैं जिन्हें दो बड़े वर्गों में विभाजित किया जा सकता है।

प्रथम श्रेणी में ऐसे उदाहरण शामिल हैं जिनमें पैरामीटर के सभी संभावित मानों के लिए समीकरण या असमानता को हल करना आवश्यक है।

दूसरी श्रेणी में ऐसे उदाहरण शामिल हैं जिनमें सभी संभावित समाधानों को नहीं खोजना आवश्यक है, लेकिन केवल वे जो कुछ अतिरिक्त शर्तों को पूरा करते हैं। ऐसी समस्याओं का वर्ग अटूट है।

ऐसी समस्याओं को हल करने के लिए विद्यार्थियों के लिए सबसे अधिक समझ में आने वाला तरीका यह है कि वे पहले सभी समाधान खोजें, और फिर उन्हें चुनें जो अतिरिक्त शर्तों को पूरा करते हैं।

मापदंडों के साथ समस्याओं को हल करते समय, सामान्य विमान (x, y) में ग्राफ़ बनाना कभी-कभी सुविधाजनक होता है, और कभी-कभी (x, a) विमान में ग्राफ़ पर विचार करना बेहतर होता है, जहाँ x एक स्वतंत्र चर है, और "a" "एक पैरामीटर है। यह मुख्य रूप से एक समस्या में संभव है जहां आपको परिचित प्राथमिक ग्राफ बनाना है: सीधी रेखाएं, पैराबोलस, सर्किल इत्यादि। इसके अलावा, रेखांकन के रेखाचित्र कभी-कभी समाधान की "प्रगति" को नेत्रहीन रूप से देखने में मदद करते हैं।

समीकरणों f (x, a) = 0 और असमानताओं f (x, a)> 0 को हल करते समय, यह याद रखना चाहिए कि, सबसे पहले, पैरामीटर के उन मूल्यों के लिए समाधान पर विचार किया जाता है जिसके लिए गुणांक वर्ग ट्रिनोमियल एफ (एक्स, ए) के उच्चतम डिग्री एक्स पर, जिससे डिग्री कम हो जाती है। द्विघात समीकरण ए (ए) एक्स 2 + B(a) x + C(a) = 0 at A(a) = 0 रैखिक हो जाता है यदि B(a) ≠ 0, और द्विघात और रैखिक समीकरणों को हल करने के तरीके अलग-अलग हैं।

द्विघात समीकरणों के साथ काम करने के लिए बुनियादी सूत्रों को याद करते हैं।

फार्म कुल्हाड़ी का समीकरण 2 + इन + सी \u003d 0, जहां एक्स  R अज्ञात हैं, a, c, c ऐसे व्यंजक हैं जो केवल प्राचलों पर निर्भर करते हैं, और a ≠ 0 को द्विघात समीकरण कहा जाता है, और D = b 2 - 4ac को एक वर्ग त्रिपद का विविक्तकर कहा जाता है।

यदि डी

यदि D > 0, तो समीकरण के दो भिन्न मूल हैं

x 1 \u003d, x 2 \u003d, और फिर ah 2 + in + c \u003d a (x - x 1) (x - x 2)।

ये जड़ें विएटा के सूत्रों द्वारा समीकरण के गुणांक के माध्यम से जुड़ी हुई हैं

यदि D = 0, तो समीकरण के दो संपाती मूल x हैं 1 \u003d x 2 \u003d, और फिर ax 2 + in + c \u003d a (x - x 1) 2 . इस मामले में, समीकरण को एक समाधान कहा जाता है।

कब, यानी \u003d 2k, द्विघात समीकरण की जड़ें सूत्र x द्वारा निर्धारित की जाती हैं 1,2 = ,

दिए गए द्विघात समीकरण x को हल करने के लिए 2 + पीएक्स + क्यू = 0

x सूत्र का प्रयोग किया जाता है 1,2 = - , साथ ही वीटा सूत्र

उदाहरण। समीकरण हल करें:

उदाहरण 1. +=

समाधान:

जब a ≠ - 1, x ≠ 2 हमें x प्राप्त होता है 2 + 2ax - 3c + 4 = 0 और मूल

एक्स 1 \u003d - ए -, एक्स 2 \u003d -ए + , पर मौजूद है

ए 2 + 2ए - 4  0, यानी पर

अब देखते हैं कि क्या कोई ऐसा है जिसके लिए या तो x 1 या एक्स 2 2 है। द्विघात समीकरण x \u003d 2 में स्थानापन्न करें, जबकि हमें a \u003d - 8 मिलता है।

इस मामले में दूसरी जड़ है(वीटा प्रमेय के अनुसार) और a = - 8 के लिए यह 14 के बराबर है।

उत्तर: a = - 8 के लिए एकमात्र समाधान x = 14 है;

यदि a  (- ∞; - 8)  (- 8; - 4)  (1; + ∞) - दो मूल x 1 और x 2;

अगर एक = - एकमात्र समाधान x =क्रमश;

यदि a  (- 4; 1), तो x   .

कभी-कभी भिन्नात्मक पदों वाले समीकरणों को घटाकर वर्गाकार कर दिया जाता है। निम्नलिखित समीकरण पर विचार करें।

उदाहरण 2. - =

हल: जब a = 0, तो इसका कोई मतलब नहीं बनता, x के मान को इन शर्तों को पूरा करना चाहिए: x -1, एक्स  -2। समीकरण के सभी पदों को a (x + 1) (x + 2) से गुणा करने पर 0,

हमें x 2 - 2 (a - 1) x + a 2 प्राप्त होता है – 2a – 3 = 0, दिए गए एक के बराबर। इसकी जड़ें:

एक्स 1 \u003d ए + 1, एक्स 2 = - 3। आइए इनमें से बाहरी जड़ों को अलग करें, अर्थात जो बराबर हैं - 1 और - 2:

एक्स 1 \u003d ए + 1 \u003d - 1, ए \u003d - 2, लेकिन ए \u003d - 2 एक्स के साथ 2 = - 5;

एक्स 1 \u003d ए + 1 \u003d - 2, ए \u003d - 3, लेकिन ए \u003d - 3 एक्स के साथ 2 = - 6;

एक्स 2 \u003d ए - 3 \u003d - 1, ए \u003d 2, लेकिन ए \u003d 2 एक्स के साथ 1 = 3;

एक्स 2 \u003d ए - 3 \u003d - 2, ए \u003d 1, लेकिन एक \u003d 1 एक्स के साथ 1 = 2.

उत्तर: जब एक ≠ 0, एक ≠ 2, a ≠ - 3, a ≠ 1 x 1 = a + 1, x 2 = a - 3;

जब एक \u003d - 2 x \u003d - 5; a \u003d - 3 x \u003d - 6 के साथ।

4. प्रारंभिक शर्तों के तहत द्विघात समीकरणों को हल करने की विधि।

पैरामीट्रिक द्विघात समीकरणों की शर्तें विविध हैं। उदाहरण के लिए, आपको उस पैरामीटर का मान खोजने की आवश्यकता है जिस पर जड़ें हैं: धनात्मक, ऋणात्मक, अलग-अलग चिन्ह हैं, कुछ संख्या से अधिक या कम, आदि। उन्हें हल करने के लिए द्विघात समीकरण ax के मूलों के गुणों का उपयोग करना चाहिए 2 + इन + सी = 0।

यदि D > 0, a > 0, तो समीकरण के दो वास्तविक भिन्न मूल हैं, जिनमें से c > 0 के चिह्न समान हैं और गुणांक के चिह्न के विपरीत हैं, और c के लिए

यदि D \u003d 0, a\u003e 0, तो समीकरण की वास्तविक और समान जड़ें हैं, जिसका चिह्न गुणांक c के चिह्न के विपरीत है।

यदि डी 0, तो समीकरण की कोई वास्तविक जड़ नहीं है।

इसी प्रकार, एक के लिए द्विघात समीकरण की जड़ों के गुण स्थापित कर सकते हैं

1. यदि हम एक द्विघात समीकरण में गुणांकों a और c को आपस में बदल दें, तो हमें एक समीकरण प्राप्त होता है, जिसकी जड़ें दिए गए समीकरण के मूलों के व्युत्क्रमानुपाती होती हैं।
2. यदि हम किसी द्विघात समीकरण में गुणांक का चिह्न बदल दें, तो हमें एक ऐसा समीकरण प्राप्त होता है, जिसके मूल दिए गए समीकरण के मूलों के विपरीत होते हैं।
3. यदि एक द्विघात समीकरण में गुणांक a और c के अलग-अलग चिन्ह हैं, तो इसकी वास्तविक जड़ें हैं।
4. यदि a > 0 और D = 0, तो द्विघात समीकरण का बायाँ पक्ष एक पूर्ण वर्ग है, और इसके विपरीत, यदि समीकरण का बायाँ पक्ष एक पूर्ण वर्ग है, तो a > 0 और D = 0।
5. यदि किसी समीकरण के सभी गुणांक परिमेय हैं और विविक्तकर एक पूर्ण वर्ग है, तो समीकरण के मूल परिमेय होते हैं।
6. यदि हम जड़ों के स्थान को शून्य के सापेक्ष मानते हैं, तो हम वीटा प्रमेय लागू करते हैं।

शर्तों के अनुसार एक वर्ग ट्रिनोमियल की जड़ों का चयन और वास्तविक रेखा पर द्विघात फलन के शून्य का स्थान।

चलो f (x) = ax 2 + in + c, a  0, मूल x 1 ˂ x 2,   ।

	संख्या रेखा पर जड़ों का स्थान।	आवश्यक और पर्याप्त स्थिति।
	एक्स 1, एक्स 2 	एफ ()> 0, डी  0, एक्स 0 
	एक्स 1, एक्स 2 > 	और f () > 0, D  0, x 0 > 
	एक्स 1  2	एक च ( )
	 1 एक्स 2  .	और f ( ) > 0, D  0, और f ( ) > 0  0  .
	 1  2	और f ( ) > 0, और f ( )
	एक्स 1  2 	एक च ( )  ) > 0
	एक्स 1   2	एक च ( )  )

उदाहरण 3 समीकरण के किन मूल्यों के लिए निर्धारित करें

एक्स 2 - 2 (ए - 1) एक्स + 2ए + 1 = 0

• कोई जड़ नहीं है

आवश्यक और पर्याप्त स्थिति D

डी \u003d (ए - 1) 2 - 2ए - 1 \u003d ए 2 - 4ए

• जड़ें हैं:

डी  0, डी \u003d (ए - 1) 2 - 2ए - 1  0, ए 

• एक जड़ है:

• दो जड़ें हैं:

डी > 0, यानी एक 

• सकारात्मक जड़ें हैं:

2(ए - 1) > 0   ए  4

यदि प्रश्न "दो सकारात्मक जड़ें" है, तो सिस्टम को प्रतिस्थापित करना चाहिएडी > 0;

• नकारात्मक जड़ें हैं:

2(ए - 1)  

• अलग-अलग संकेतों की जड़ें हैं, यानी। एक सकारात्मक है और दूसरा नकारात्मक है:

  ए ;

स्थिति इसका उपयोग करना आवश्यक नहीं है, यह पर्याप्त x है 1 एक्स 2

• जड़ों में से एक 0 के बराबर है:

एक आवश्यक पर्याप्त स्थिति समीकरण के मुक्त पद के शून्य के बराबर है, अर्थात 2ए + 1 = 0, ए = -1/2।

दूसरी जड़ का चिन्ह या तो मूल समीकरण a = -1/2 में प्रतिस्थापन द्वारा निर्धारित किया जाता है, या, अधिक सरलता से, वीटा प्रमेय x द्वारा 1 + एक्स 2 \u003d 2 (ए - 1), और \u003d -1/2 को प्रतिस्थापित करने के बाद, हमें एक्स मिलता है 2 = - 3, अर्थात् एक \u003d -1/2 दो जड़ों के साथ: x 1 \u003d 0, x 2 \u003d - 3।

उदाहरण 4 . पैरामीटर के किन मूल्यों पर समीकरण

(ए - 2) एक्स 2 – 4ax +3 -2a = 0 का एक अनूठा हल है जो असमानता x को संतुष्ट करता है

समाधान।

विविक्तकर 2 - (a - 2) (3 - 2a)

4ए 2 - 3ए + 6 + 2ए 2 - 4ए = 6ए 2 - 7ए + 6

चूंकि 49 - 144 \u003d - 95 और पहला कारक 6 हैतो 6a 2 - 7a + 6 सबके लिए x  R.

तब x 1,2 = .

समस्या की स्थिति के अनुसार x2, तो हमें असमानता मिलती है

अपने पास:

सभी के लिए सत्य a  R.

6ए 2 - 7ए + 6 6ए 2 - 7ए - 10 2

और 1,2 \u003d 1/12 (7  17), और 1 \u003d 2, और 2 \u003d - 5/6।

इसलिए, -5/6

उत्तर: -

5. एक समान चर के रूप में पैरामीटर।

सभी कार्यों मेंपैरामीटर को एक निश्चित लेकिन अज्ञात संख्या के रूप में माना गया था। इस बीच, एक औपचारिक दृष्टिकोण से, एक पैरामीटर एक चर है, इसके अलावा, उदाहरण में मौजूद अन्य लोगों के साथ "बराबर" है। उदाहरण के लिए, फॉर्म पैरामीटर f (x; a) के इस दृश्य के साथ, फ़ंक्शंस को एक (पहले की तरह) नहीं, बल्कि दो चर के साथ परिभाषित किया गया है। इस तरह की व्याख्या स्वाभाविक रूप से मापदंडों के साथ समस्याओं का एक और प्रकार (अधिक सटीक, एक समाधान विधि जो इस प्रकार को निर्धारित करती है) बनाती है। आइए हम इस प्रकार का एक विश्लेषणात्मक समाधान दिखाते हैं।

उदाहरण 5 Xy विमान पर, उन सभी बिंदुओं को इंगित करें जिनके माध्यम से परिवार y \u003d x का कोई भी वक्र नहीं गुजरता है 2 - 4पीएक्स + 2पी 2 – 3, जहाँ p एक प्राचल है।

हल: यदि (x 0; y 0 ) एक बिंदु है जिससे दिए गए परिवार का कोई भी वक्र नहीं गुजरता है, तो इस बिंदु के निर्देशांक मूल समीकरण को संतुष्ट नहीं करते हैं। नतीजतन, समस्या को x और y के बीच संबंध खोजने तक सीमित कर दिया गया, जिसके तहत स्थिति में दिए गए समीकरण का कोई समाधान नहीं होगा। चर x और y पर ध्यान केंद्रित करके नहीं, बल्कि पैरामीटर p पर ध्यान केंद्रित करके वांछित निर्भरता प्राप्त करना आसान है। इस मामले में, एक उत्पादक विचार उत्पन्न होता है: दिए गए समीकरण को p में द्विघात के रूप में मानें। अपने पास

2p 2 - 4px + x 2 – y – 3 = 0. विविक्तकर= 8x 2 + 8y + 24 ऋणात्मक होना चाहिए। यहाँ से हमें y˂ - x प्राप्त होता है 2 - 3, इसलिए, वांछित सेट पैराबोला y \u003d - x के "अंडर" लेटे हुए समन्वय विमान के सभी बिंदु हैं 2 – 3.

उत्तर: पर 2 – 3

6. मापदंडों के साथ द्विघात असमानताओं को हल करने की तकनीक

सामान्य रूप में।

स्क्वायर (सख्त और गैर-सख्त) असमानताएं कहलाती हैं

अनुमत पैरामीटर के वे मान हैं जिनके लिए ए, बी, सी मान्य हैं। द्विघात असमानताओं को या तो विश्लेषणात्मक या ग्राफिक रूप से हल करना सुविधाजनक है। चूँकि द्विघात फलन का ग्राफ एक परवलय है, तो a> 0 के लिए परवलय की शाखाएँ ऊपर की ओर निर्देशित होती हैं, a के लिए

परवलय की विभिन्न स्थितियाँ f (x) = ax 2 + इन + एस, ए  a > 0 के लिए 0 चित्र 1 में दिखाया गया है

ए) सी) सी)

ए) अगर एफ (एक्स)> 0 और डी  आर;

ख) यदि f (x) > 0 और D = 0, तो x ;

ग) यदि f (x) > 0 और D > 0, तो x (-  ; x 1 )  ( x 2 ; +  )।

परवलय की स्थितियों को a के लिए समान रूप से माना जाता है

उदाहरण के लिए, तीन मामलों में से एक जहां

जब a 0 और f (x) > 0 x  (x 1; x 2);

a 0 और f (x)  (-  ; x 1 )  (x 2 ; +  ) पर।

एक उदाहरण के रूप में, असमानता के समाधान पर विचार करें।

उदाहरण 6 असमानता x को हल करें 2 + 2x + ए> 0।

माना D त्रिपद x का विविक्तकर है 2 + 2x + a > 0. D = 0 के लिए, a = 1 के लिए, असमानता रूप लेती है:

(एक्स + 1) 2> 0

यह x = - 1 को छोड़कर, x के किसी भी वास्तविक मान के लिए सत्य है।

डी > 0 के लिए, यानी एक्स पर, ट्रिनोमियल एक्स 2 + 2x + a के दो मूल हैं: - 1 -और

1 + और असमानता का समाधान अंतराल है

(-  ; - 1 – )  (- 1 + ; +  )

इस असमानता को रेखांकन द्वारा हल करना आसान है। ऐसा करने के लिए, हम इसे फॉर्म में दर्शाते हैं

एक्स 2 + 2x> - ए

और फ़ंक्शन y = x प्लॉट करें 2 + 2x

सीधी रेखा y \u003d - a के साथ इस ग्राफ के चौराहे के बिंदुओं के भुज और समीकरण x की जड़ें हैं 2 + 2x = - ए।

उत्तर:

-a > - 1 के साथ, यानी एक पर, x  (-  ; x 1 )  (x 2 ;+  );

पर - ए = - 1, यानी a = 1 के साथ, x कोई भी वास्तविक संख्या है, सिवाय - 1 के;

पर - ए , यानी a > 1 के लिए, x कोई भी वास्तविक संख्या है।

उदाहरण 7 . असमानता cx को हल करें 2 - 2 (एस - 1) एक्स + (एस + 2)

जब c \u003d 0, यह रूप लेता है: 2x + 2समाधान एक्स है

हम संकेतन f (x) = cx का परिचय देते हैं 2 - 2 (एस - 1) एक्स + (एस + 2)जहां सी ≠ 0।

इस स्थिति में, असमानता f (x)

मान लीजिए D, f(x) का विविक्तकर है। 0.25 डी = 1 - 4s।

यदि D > 0, अर्थात अगर साथ> 0.25, तब f (x) का चिन्ह x के किसी भी वास्तविक मान के लिए c के चिन्ह के साथ मेल खाता है, अर्थात च (एक्स)किसी भी x  R के लिए > 0, इसलिए, c > के लिए 0.25 असमानता एफ (एक्स)

अगर डी = 0, यानी सी \u003d 0.25, फिर एफ (एक्स) \u003d (0.25 x + 1.5) 2, अर्थात् f (x)  0 किसी के लिए भी

एक्स  आर। इसलिए, सी = 0.25 के लिए, असमानता एफ (एक्स)

मामले D पर विचार करें 0). f (x) = 0 x के दो वास्तविक मानों के लिए:

x 1 \u003d (s - 1 -) और x 2 \u003d (s - 1 +)।

यहां दो मामले हो सकते हैं:

असमानता f(x) को हल करें

f (x) c के चिन्ह के साथ मेल खाता है। इस प्रश्न का उत्तर देने के लिए, ध्यान दें कि - , अर्थात। एस - 1 - ˂ एस - 1 + , लेकिन चूंकि (के साथ - 1 - ) (एस - 1 + ) और इसलिए असमानता का समाधान होगा:

(- ; (एस - 1 - ))  ( (एस - 1 + ); +  )।

अब, असमानता को हल करने के लिए, यह c के उन मानों को इंगित करने के लिए पर्याप्त है जिनके लिए f (x) का चिह्न c के चिह्न के विपरीत है। चूंकि 0 1 पर 2, फिर x  (x 1; x 2)।

उत्तर: c = 0 x  R पर;

साथ  (-  ; x 2 )  ( x 1 ; +  );

0 पर  (x 1; x 2);

с  0.25 के लिए कोई समाधान नहीं हैं।

एक समान चर के रूप में पैरामीटर का दृश्य हल करने और द्विघात असमानताओं के चित्रमय तरीकों में परिलक्षित होता है। दरअसल, चूंकि चर के साथ पैरामीटर "अधिकारों के बराबर" है, इसलिए इसके लिए अपने स्वयं के समन्वय अक्ष को "आवंटित" करना स्वाभाविक है। इस प्रकार, एक निर्देशांक तल (x; a) उत्पन्न होता है। अक्षों को निरूपित करने के लिए x और y अक्षरों की पारंपरिक पसंद की अस्वीकृति के रूप में इस तरह के एक मामूली विवरण, मापदंडों के साथ समस्याओं को हल करने के लिए सबसे प्रभावी तरीकों में से एक को परिभाषित करता है।

यह तब सुविधाजनक होता है जब समस्या में एक पैरामीटर a और एक चर x होता है। समाधान प्रक्रिया ही इस तरह दिखती है। सबसे पहले, एक चित्रमय छवि का निर्माण किया जाता है, फिर परिणामी ग्राफ को पैरामीट्रिक अक्ष के लंबवत सीधी रेखाओं के साथ पार करते हुए, हम आवश्यक जानकारी को "हटा" देते हैं।

अक्षों को निरूपित करने के लिए x और y अक्षरों की पारंपरिक पसंद की अस्वीकृति मापदंडों के साथ समस्याओं को हल करने के लिए सबसे प्रभावी तरीकों में से एक निर्धारित करती है - "डोमेन विधि"

1. प्रारंभिक परिस्थितियों में द्विघात असमानताओं को हल करने की विधि।

आइए मापदंडों के साथ एक द्विघात असमानता के विश्लेषणात्मक समाधान पर विचार करें, जिसके परिणाम वास्तविक रेखा पर माने जाते हैं।

उदाहरण 8

असमानता वाले प्रत्येक के लिए सभी x मान ज्ञात कीजिए

(2-एक्स)ए 2 + (एक्स 2 -2एक्स + 3)ए-3x≥0

अंतराल [-3; 0] से संबंधित किसी भी मूल्य के लिए प्रदर्शन किया जाता है।

समाधान। हम इस असमानता के बाएँ पक्ष को इस प्रकार रूपांतरित करते हैं:

(2-x) a 2 + (x 2 -2x + 3) a-3x \u003d ax 2 - a 2 x - 2ax + 2a 2 + 3a - 3x \u003d

कुल्हाड़ी (x - a) -2a (x - a) - 3 (x-a) \u003d (x - a) (ax - 2a - 3)।

यह असमानता रूप लेगी: (x - a) (ax - 2a - 3) ≥ 0।

यदि a = 0, तो हमें - Зх ≥ 0 x ≤ 0 मिलता है।

यदि a≠ 0, तो -3 a

क्योंकि ए 0, तो इस असमानता का समाधान संख्यात्मक अक्ष का अंतराल होगा, जो असमानता के अनुरूप समीकरण की जड़ों के बीच स्थित है।

आइए संख्याओं की पारस्परिक व्यवस्था का पता लगाएंएक और स्थिति को ध्यान में रखते हुए - 3 ≤ ए

3 ≤ए

ए = -1।

सभी मामलों में, हम पैरामीटर के मूल्यों के आधार पर इस असमानता का समाधान प्रस्तुत करते हैं:

हम पाते हैं कि प्राचल a के किसी भी मान के लिए केवल x = -1 ही इस असमानता का हल है .

उत्तर 1

8. निष्कर्ष।

मुझे "पैरामीटर के साथ द्विघात समीकरणों और असमानताओं को हल करने के लिए पद्धति संबंधी सिफारिशों का विकास" विषय पर एक परियोजना क्यों चुना गया था? चूंकि किसी भी त्रिकोणमितीय, घातीय, लघुगणकीय समीकरणों, असमानताओं, प्रणालियों को हल करते समय, हम अक्सर कभी-कभी रैखिक, और अक्सर द्विघात समीकरणों और असमानताओं पर विचार करते हैं। पैरामीटर के साथ सबसे जटिल समस्याओं को हल करते समय, अधिकांश कार्यों को प्रकार के समाधानों की पसंद के समकक्ष परिवर्तनों की सहायता से घटाया जाता है: ए (एक्स - ए) (एक्स - सी)> 0 (

हमने द्विघात समीकरणों और असमानताओं को मापदंडों के साथ हल करने के लिए सैद्धांतिक आधारों पर विचार किया है। हमने आवश्यक सूत्रों और परिवर्तनों को याद किया, विभेदक के मूल्य के आधार पर द्विघात फ़ंक्शन के ग्राफ़ की विभिन्न व्यवस्थाओं पर विचार किया, उच्चतम गुणांक पर संकेत पर, जड़ों के स्थान पर, परवलय के शीर्ष पर। हमने परिणामों को हल करने और चुनने के लिए एक योजना की पहचान की, एक तालिका संकलित की।

परियोजना द्विघात समीकरणों और असमानताओं को हल करने के लिए विश्लेषणात्मक और चित्रमय तरीके दिखाती है। एक व्यावसायिक स्कूल में छात्रों को सामग्री के बेहतर आत्मसात करने के लिए सामग्री की दृश्य धारणा की आवश्यकता होती है। यह दिखाया गया है कि आप चर x को कैसे बदल सकते हैं और पैरामीटर को समान मान के रूप में स्वीकार कर सकते हैं।

इस विषय के एक दृश्य आत्मसात के लिए, प्रत्येक अनुभाग के लिए 1-2 मापदंडों के साथ 8 कार्यों के समाधान पर विचार किया जाता है। उदाहरण संख्या 1 में, पैरामीटर के विभिन्न मूल्यों के समाधान की संख्या पर विचार किया जाता है, उदाहरण संख्या 3 में, विभिन्न प्रारंभिक स्थितियों के लिए द्विघात समीकरण के समाधान का विश्लेषण किया जाता है। द्विघात असमानताओं को हल करने के लिए एक ग्राफिक चित्रण बनाया गया है। उदाहरण संख्या 5 में, पैरामीटर को समान मान के रूप में बदलने की विधि का उपयोग किया जाता है। परियोजना में परीक्षा उत्तीर्ण करने के लिए गहन तैयारी के लिए खंड सी में शामिल कार्यों से उदाहरण संख्या 8 पर विचार करना शामिल है।

मापदंडों के साथ समस्याओं को हल करने में छात्रों के उच्च-गुणवत्ता वाले प्रशिक्षण के लिए, मल्टीमीडिया तकनीकों का पूर्ण रूप से उपयोग करने की सिफारिश की जाती है, अर्थात्: व्याख्यान, इलेक्ट्रॉनिक पाठ्यपुस्तकों और पुस्तकों के लिए प्रस्तुतियों का उपयोग, मीडिया लाइब्रेरी से स्वयं के विकास। गणित+कंप्यूटर विज्ञान के बाइनरी पाठ बहुत प्रभावी होते हैं। इंटरनेट शिक्षक और छात्र के लिए एक अपूरणीय सहायक है। प्रस्तुति के लिए मौजूदा शैक्षिक संसाधनों से आयातित वस्तुओं की आवश्यकता होती है। काम में सबसे सुविधाजनक और स्वीकार्य डीईआर "स्कूल में माइक्रोसॉफ्ट ऑफिस का उपयोग करना" है।

इस विषय पर पद्धति संबंधी सिफारिशों के विकास से स्कूल में काम करने वाले युवा शिक्षकों के काम में आसानी होगी, शिक्षक के पोर्टफोलियो को फिर से भरेंगे, विशेष विषयों के लिए एक मॉडल के रूप में काम करेंगे, नमूना समाधान छात्रों को जटिल कार्यों से निपटने में मदद करेंगे।

9. साहित्य।

1. गोर्शेटिन पी.आई., पोलोंस्की वी.बी., याकिर एम.एस. मापदंडों के साथ कार्य। "इलेक्सा", "व्यायामशाला", मास्को - खार्कोव, 2002।

2. बालयान ई.एन. परीक्षा और ओलंपियाड की तैयारी के लिए गणित में कार्यों का संग्रह। 9-11 ग्रेड। "फीनिक्स", रोस्तोव-ऑन-डॉन, 2010।

3. यास्त्रेबिनेत्स्की जी.ए. मापदंडों के साथ कार्य। एम।, "ज्ञान", 1986।

4. कोलेनिकोवा एस.आई. अंक शास्त्र। एकीकृत राज्य परीक्षा की जटिल समस्याओं का समाधान। एम। "आईआरआईएस - प्रेस", 2005।

5. रोडियोनोव ई.एम., सिन्याकोवा एस.एल. अंक शास्त्र। विश्वविद्यालयों में प्रवेश के लिए भत्ता। प्रशिक्षण केंद्र "लैंडमार्क" MSTU। एन.ई. बाउमन, एम., 2004।

6. स्कैनवी एम.आई. विश्वविद्यालयों के आवेदकों के लिए गणित में कार्यों का संग्रह: 2 पुस्तकों में। पुस्तक 1, एम।, 2009।

असमानता

(ए, बी, सी, …,, x)>(ए, बी, सी, …, एक्स), (1)

जहां ए, बी, सी, …,पैरामीटर हैं और x एक वास्तविक चर है जिसे असमानता कहा जाता है जिसमें एक अज्ञात पैरामीटर होता है।

पैरामीटर मानों की कोई भी प्रणाली a = a 0 , बी = बी 0 , सी = सी 0 , …, के = के 0 , किसी समारोह के लिए

(ए, बी, सी, …,, एक्स) और

(ए, बी, सी, …,, एक्स

वास्तविक संख्या के क्षेत्र में समझ में आता है, स्वीकार्य पैरामीटर मानों की प्रणाली कहा जाता है।

x का वैध मान कहा जाता है यदि

(ए, बी, सी, …,, एक्स) और

(ए, बी, सी, …,, एक्स

पैरामीटर मानों की किसी भी स्वीकार्य प्रणाली के लिए वास्तविक मान लें।

एक्स के सभी स्वीकार्य मूल्यों के सेट को असमानता (1) का डोमेन कहा जाता है।

एक वास्तविक संख्या x 0 को असमानता (1) का एक विशेष समाधान कहा जाता है यदि असमानता

(ए, बी, सी, …,, एक्स 0 )>(ए, बी, सी, …, एक्स 0 )

स्वीकार्य पैरामीटर मानों की किसी भी प्रणाली के लिए सत्य है।

असमिका के सभी विशेष हलों के समुच्चय (1) को इस असमिका का व्यापक हल कहते हैं।

असमानता को हल करने के लिए (1) का अर्थ यह इंगित करना है कि मापदंडों के किन मूल्यों के लिए एक सामान्य समाधान है और यह क्या है।

दो असमानताएँ

(ए, बी, सी, …,, x)>(ए, बी, सी, …, एक्स) और (1)

(ए, बी, सी, …,, x)>(ए, बी, सी, …, एक्स) (2)

समतुल्य कहा जाता है यदि उनके पास स्वीकार्य पैरामीटर मानों की प्रणालियों के समान सेट के लिए समान सामान्य समाधान हैं।

समाधान एल्गोरिथ्म।

इस असमानता की परिभाषा का डोमेन खोजें।

हम असमानता को एक समीकरण में कम करते हैं।

हम a को x के फलन के रूप में व्यक्त करते हैं।

X0a समन्वय प्रणाली में, हम x के उन मानों के लिए a = (x) फ़ंक्शंस के ग्राफ़ बनाते हैं जो इस असमानता की परिभाषा के डोमेन में शामिल हैं।

हम इस असमानता को संतुष्ट करने वाले बिंदुओं के समूह पाते हैं।

हम परिणाम पर पैरामीटर के प्रभाव की जांच करते हैं।

रेखांकन के प्रतिच्छेदन बिंदुओं के भुज ज्ञात कीजिए।

लाइन को a=const सेट करें और हम इसे - से + में शिफ्ट कर देंगे

हम उत्तर लिखते हैं।

यह x0a समन्वय प्रणाली का उपयोग करके मापदंडों के साथ असमानताओं को हल करने के लिए एल्गोरिदम में से एक है। मानक xOy निर्देशांक प्रणाली का उपयोग करके समाधान के अन्य तरीके भी संभव हैं।

3. उदाहरण

I. पैरामीटर ए के सभी स्वीकार्य मूल्यों के लिए, असमानता को हल करें

असमानताओं की प्रणाली द्वारा परिभाषित पैरामीटर के डोमेन में

यह असमानता असमानताओं की प्रणाली के बराबर है

यदि, तो मूल असमानता के समाधान खंड भरते हैं।

उत्तर:, .

द्वितीय। पैरामीटर के किन मूल्यों के लिए सिस्टम के पास समाधान है

असमिका के बाईं ओर स्थित त्रिपद के मूल ज्ञात कीजिए -

समानताएं (*) द्वारा दी गई सीधी रेखाएं ए0एक्स समन्वय विमान को चार क्षेत्रों में विभाजित करती हैं, जिनमें से प्रत्येक में एक वर्ग ट्रिनोमियल होता है

एक स्थिर चिह्न रखता है। समीकरण (2) मूल बिंदु पर केंद्रित त्रिज्या 2 के एक चक्र को परिभाषित करता है। फिर मूल प्रणाली का समाधान चौराहा छायांकित होगा

एक वृत्त के साथ एक वृत्त, जहाँ, और मान और सिस्टम से पाए जाते हैं

और मान और सिस्टम से पाए जाते हैं

इन प्रणालियों को हल करने से हमें वह मिलता है

तृतीय। पैरामीटर ए के मूल्यों के आधार पर असमानता को हल करें।

हम स्वीकार्य मूल्यों का क्षेत्र पाते हैं -

आइए xOy निर्देशांक प्रणाली में फ़ंक्शन का एक ग्राफ़ बनाएं।

जब असमानता का कोई समाधान नहीं है।

समाधान के लिए x संबंध को संतुष्ट करता है, जहाँ

एक पैरामीटर के साथ असमानताओं को हल करना।

असमानताएँ जिनका रूप ax > b, ax है< b, ax ≥ b, ax ≤ b, где a и b – действительные числа или выражения, зависящие от параметров, а x – неизвестная величина, называются रैखिक असमानताएँ.

पैरामीटर के साथ रैखिक असमानताओं को हल करने के सिद्धांत पैरामीटर के साथ रैखिक समीकरणों को हल करने के सिद्धांतों के समान ही हैं।

उदाहरण 1

असमिका 5x - a > ax + 3 को हल कीजिए।

समाधान।

सबसे पहले, आइए मूल असमानता को बदलें:

5x - ax > a + 3, हम असमानता के बाईं ओर कोष्ठक से x निकालते हैं:

(5 - ए) एक्स> ए + 3। अब पैरामीटर ए के लिए संभावित मामलों पर विचार करें:

यदि a > 5 तो x< (а + 3) / (5 – а).

यदि a = 5, तो कोई हल नहीं है।

यदि एक< 5, то x >(ए + 3) / (5 - ए)।

यह समाधान असमानता का उत्तर होगा।

उदाहरण 2

असमानता x(a - 2) / (a ​​- 1) - 2a / 3 ≤ 2x - a को a ≠ 1 के लिए हल करें।

समाधान।

आइए मूल असमानता को बदलें:

एक्स (ए - 2) / (ए - 1) - 2x ≤ 2ए/3 - ए;

आह/(ए - 1) ≤ -ए/3. असमानता के दोनों भागों को (-1) से गुणा करने पर, हम पाते हैं:

कुल्हाड़ी/(ए - 1) ≥ ए/3। आइए पैरामीटर ए के संभावित मामलों का पता लगाएं:

1 मामला। मान लीजिए a/(a – 1) > 0 या a € (-∞; 0)ᴗ(1; +∞). फिर x ≥ (ए - 1)/3।

दूसरा मामला। माना a/(a – 1) = 0, अर्थात a = 0. तब x कोई वास्तविक संख्या है।

तीसरा मामला। माना a/(a – 1)< 0 или а € (0; 1). Тогда x ≤ (а – 1)/3.

उत्तर: एक्स € ​​[(ए - 1) / 3; +∞) एक € (-∞; 0)ᴗ(1; +∞) के लिए;
एक्स € ​​[-∞; (ए - 1)/3] € (0; 1) के लिए;
x € आर एक = 0 के लिए।

उदाहरण 3

असमिका को हल करें |1 + x| ≤ एक्स के संबंध में कुल्हाड़ी।

समाधान।

यह इस शर्त से अनुसरण करता है कि असमानता कुल्हाड़ी का दाहिना पक्ष गैर-नकारात्मक होना चाहिए, अर्थात ax ≥ 0. असमानता से मॉड्यूल के विस्तार के नियम से |1 + x| ≤ कुल्हाड़ी हमारे पास दोहरी असमानता है

कुल्हाड़ी ≤ 1 + x ≤ कुल्हाड़ी। हम परिणाम को एक प्रणाली के रूप में फिर से लिखते हैं:

(कुल्हाड़ी ≥ 1 + x;
(-ax ≤ 1 + x.

आइए फॉर्म में बदलें:

((ए - 1)x ≥ 1;
((ए + 1)x ≥ -1।

हम अंतराल पर और बिंदुओं पर परिणामी प्रणाली की जांच करते हैं (चित्र .1):

a ≤ -1 x € (-∞; 1/(a - 1)] के लिए।

1 पर< а < 0 x € [-1/(а – 1); 1/(а – 1)].

जब एक \u003d 0 x \u003d -1।

0 पर< а ≤ 1 решений нет.

असमानताओं को हल करने के लिए ग्राफिकल विधि

प्लॉटिंग एक पैरामीटर वाले समीकरणों के समाधान को बहुत सरल करता है। एक पैरामीटर के साथ असमानताओं को हल करने में ग्राफिकल विधि का उपयोग और भी स्पष्ट और अधिक समीचीन है।

प्रपत्र की असमानताओं का ग्राफिकल समाधान f(x) ≥ g(x) का अर्थ है चर x के मानों का पता लगाना जिसके लिए फ़ंक्शन f(x) का ग्राफ़ फ़ंक्शन g(x) के ग्राफ़ के ऊपर स्थित है। ऐसा करने के लिए, रेखांकन के प्रतिच्छेदन बिंदुओं को खोजना हमेशा आवश्यक होता है (यदि वे मौजूद हैं)।

उदाहरण 1

असमानता को हल करें |x + 5|< bx.

समाधान।

हम फ़ंक्शन y = |x + 5| का ग्राफ़ बनाते हैं और वाई = बीएक्स (अंक 2). असमिका का समाधान चर x के वे मान होंगे जिनके लिए फलन y = |x + 5| फलन y = bx के ग्राफ के नीचे होगा।

आंकड़ा दिखाता है:

1) b > 1 के लिए, रेखाएँ प्रतिच्छेद करती हैं। इन कार्यों के ग्राफ के चौराहे बिंदु का भुज समीकरण x + 5 = bx का समाधान है, जहां से x = 5/(b - 1)। ग्राफ y \u003d bx अंतराल (5 / (b - 1); +∞) से x के लिए अधिक है, जिसका अर्थ है कि यह सेट असमानता का समाधान है।

2) इसी प्रकार, हम पाते हैं कि -1 पर< b < 0 решением является х из интервала (-5/(b + 1); 5/(b – 1)).

3) b ≤ -1 x € (-∞; 5/(b - 1)) के लिए।

4) 0 ≤ b ≤ 1 के लिए, ग्राफ़ प्रतिच्छेद नहीं करते हैं, जिसका अर्थ है कि असमानता का कोई समाधान नहीं है।

उत्तर: x € (-∞; 5/(बी - 1)) बी ≤ -1 के लिए;
x € (-5/(बी + 1); 5/(बी - 1)) -1 पर< b < 0;
0 ≤ b ≤ 1 के लिए कोई समाधान नहीं है; x € (5/(b – 1); +∞) b > 1 के लिए।

उदाहरण 2

असमिका a(a + 1)x > (a + 1)(a + 4) को हल कीजिए।

समाधान।

1) आइए पैरामीटर a के लिए "नियंत्रण" मान खोजें: a 1 = 0, a 2 = -1।

2) वास्तविक संख्याओं के प्रत्येक उपसमुच्चय पर इस असमानता को हल करते हैं: (-∞; -1); (-1); (-10); (0); (0; + ∞)।

ए) ए< -1, из данного неравенства следует, что х >(ए + 4)/ए;

बी) ए \u003d -1, तो यह असमानता 0 x> 0 का रूप ले लेगी - कोई समाधान नहीं हैं;

सी) -1< a < 0, из данного неравенства следует, что х < (a + 4)/a;

d) a = 0, तो इस असमानता का रूप 0 x > 4 है - कोई समाधान नहीं है;

e) a > 0, इस असमानता का अर्थ है कि x > (a + 4)/a.

उदाहरण 3

असमानता को हल करें |2 – |x||< a – x.

समाधान।

हम फ़ंक्शन y = |2 – |x|| प्लॉट करते हैं (चित्र 3)और रेखा y \u003d -x + a के स्थान के सभी संभावित मामलों पर विचार करें।

उत्तर: असमानता का a ≤ -2 के लिए कोई समाधान नहीं है;
x € (-∞; (a - 2)/2) with a € (-2; 2];
x € (-∞; (a + 2)/2) a> 2 के लिए।

विभिन्न समस्याओं, समीकरणों और असमानताओं को मापदंडों के साथ हल करते समय, महत्वपूर्ण संख्या में अनुमानी तकनीकें खुलती हैं, जिन्हें तब गणित की किसी भी अन्य शाखा में सफलतापूर्वक लागू किया जा सकता है।

मापदंडों के साथ समस्याएं तार्किक सोच और गणितीय संस्कृति के निर्माण में महत्वपूर्ण भूमिका निभाती हैं। इसीलिए, मापदंडों के साथ समस्याओं को हल करने के तरीकों में महारत हासिल करने के बाद, आप अन्य समस्याओं का सफलतापूर्वक सामना करेंगे।

क्या आपका कोई प्रश्न है? असमानताओं को हल करने का तरीका नहीं जानते?
ट्यूटर की मदद लेने के लिए - रजिस्टर करें।
पहला पाठ मुफ़्त है!

साइट, सामग्री की पूर्ण या आंशिक प्रतिलिपि के साथ, स्रोत के लिए एक लिंक आवश्यक है।

राज्य के बजटीय शैक्षिक संस्थान

समारा क्षेत्र माध्यमिक सामान्य शिक्षा

स्कूल नंबर 2 आई.एम. वी। मास्किना रेलवे कला। Klyavlino

नगरपालिका जिला Klyavlinsky

समारा क्षेत्र

« समीकरण

और

असमानता

मापदंडों के साथ"

ट्यूटोरियल

Klyavlino

ट्यूटोरियल

"पैरामीटर के साथ समीकरण और असमानताएं"कक्षा 10-11 के छात्रों के लिए

यह मैनुअल वैकल्पिक पाठ्यक्रम "पैरामीटर के साथ समीकरण और असमानता" के कार्यक्रम का एक परिशिष्ट है, जिसने एक बाहरी परीक्षा उत्तीर्ण की है (19 दिसंबर, 2008 को समारा क्षेत्र के शिक्षा और विज्ञान मंत्रालय की वैज्ञानिक और पद्धति विशेषज्ञ परिषद की सिफारिश की गई थी) समारा क्षेत्र के शैक्षणिक संस्थानों में उपयोग के लिए)

लेखक

रोमाडानोवा इरीना व्लादिमीरोवाना

गणित शिक्षक, Klyavlinskaya माध्यमिक सामान्य शिक्षा

स्कूल नंबर 2 उन्हें। वी। मास्किना, क्लाईवलिंस्की जिला, समारा क्षेत्र

सर्बायेवा इरीना अलेक्सेवना

परिचय ……………………………………………………… 3-4

रेखीय समीकरण और पैरामीटर के साथ असमानताएं ……………..4-7

द्विघात समीकरण और पैरामीटर के साथ असमानताएं …………… 7-9

प्राचलों के साथ भिन्नात्मक परिमेय समीकरण ……………..10-11

तर्कहीन समीकरण और पैरामीटर के साथ असमानताएं …… 11-13

त्रिकोणमितीय समीकरण और पैरामीटर के साथ असमानताएँ। 14-15

पैरामीटर के साथ घातीय समीकरण और असमानताएं ………16-17

लघुगणकीय समीकरण और पैरामीटर के साथ असमानताएं ...... 16-18

एकीकृत राज्य परीक्षा के कार्य……………………………………………………18-20

स्वतंत्र कार्य के लिए कार्य …………………………… 21-28

परिचय।

पैरामीटर के साथ समीकरण और असमानताएं।

यदि किसी समीकरण या असमानता में कुछ गुणांक विशिष्ट संख्यात्मक मानों द्वारा नहीं दिए जाते हैं, लेकिन अक्षरों द्वारा इंगित किए जाते हैं, तो वे कहलाते हैं पैरामीटर,और समीकरण या असमानता ही पैरामीट्रिक।

मापदंडों के साथ एक समीकरण या असमानता को हल करने के लिए, आपको यह करना होगा:

प्रमुखता से दिखाना विशेष अर्थ- यह उस पैरामीटर का मान है जिसमें या जिसके माध्यम से गुजरने पर समीकरण या असमानता का समाधान बदल जाता है।

परिभाषित करना अनुमत मानवे पैरामीटर मान हैं जिन पर समीकरण या असमानता समझ में आती है।

मापदंडों के साथ एक समीकरण या असमानता को हल करने का अर्थ है:

1) यह निर्धारित करें कि पैरामीटर समाधान के कौन से मूल्य मौजूद हैं;

2) पैरामीटर मानों की प्रत्येक स्वीकार्य प्रणाली के लिए, समाधानों का संगत सेट खोजें।

एक पैरामीटर के साथ एक समीकरण को निम्नलिखित तरीकों से हल किया जा सकता है: विश्लेषणात्मक या ग्राफिकल।

विश्लेषणात्मक विधि कई मामलों पर विचार करके समीकरण की जांच करने का कार्य मानता है, जिनमें से कोई भी छूट नहीं सकता है।

विश्लेषणात्मक पद्धति द्वारा प्रत्येक प्रकार के मापदंडों के साथ समीकरण और असमानता के समाधान में स्थिति का विस्तृत विश्लेषण और एक सुसंगत अध्ययन शामिल है, जिसके दौरान आवश्यकता उत्पन्न होती है "कोमल हैंडलिंग"एक पैरामीटर के साथ।

ग्राफिक विधि इसमें समीकरण के एक ग्राफ का निर्माण शामिल है, जिसके द्वारा यह निर्धारित करना संभव है कि क्रमशः, पैरामीटर में परिवर्तन समीकरण के समाधान को कैसे प्रभावित करता है। ग्राफ कभी-कभी किसी को निर्धारित कार्यों को हल करने के लिए आवश्यक और पर्याप्त शर्तों को विश्लेषणात्मक रूप से तैयार करने की अनुमति देता है। ग्राफिकल समाधान विधि विशेष रूप से प्रभावी होती है जब पैरामीटर के आधार पर समीकरण की कितनी जड़ें स्थापित करना आवश्यक होता है और इसे नेत्रहीन रूप से देखने का निस्संदेह लाभ होता है।

§ 1. रैखिक समीकरण और असमानताएं।

रेखीय समीकरण ए एक्स = बी , सामान्य रूप में लिखा गया, पैरामीटर के साथ एक समीकरण के रूप में माना जा सकता है, जहां एक्स - अज्ञात , ए , बी - विकल्प। इस समीकरण के लिए, पैरामीटर का विशेष या नियंत्रण मूल्य वह है जिस पर अज्ञात में गुणांक गायब हो जाता है।

एक पैरामीटर के साथ एक रेखीय समीकरण को हल करते समय, मामलों पर विचार किया जाता है जब पैरामीटर इसके विशेष मूल्य के बराबर होता है और इससे अलग होता है।

विशेष पैरामीटर मान ए मूल्य है ए = 0.

बी = 0 एक विशेष पैरामीटर मान है बी .

पर बी ¹ 0 समीकरण का कोई हल नहीं है।

पर बी = 0 समीकरण रूप लेगा: 0x = 0. इस समीकरण का हल कोई वास्तविक संख्या है।

रूप की असमानता आह > बी और कुल्हाड़ी < बी (ए ≠ 0)रैखिक असमानताएँ कहलाती हैं। असमानता के समाधान का सेट आह >बी- अंतर

(; +), अगर ए > 0 , और (-;) , अगर ए< 0 . इसी तरह असमानता के लिए

ओह< बी समाधान का सेट - अंतराल(-;), अगर ए > 0, और (; +), अगर ए< 0.

उदाहरण 1 प्रश्न हल करें कुल्हाड़ी = 5

समाधान: यह एक रैखिक समीकरण है।

अगर ए = 0, फिर समीकरण 0 × एक्स = 5कोई समाधान नहीं है।

अगर ए¹ 0, एक्स =- समीकरण का समाधान।

उत्तर: पर ए¹ 0, एक्स =

a = 0 के लिए कोई हल नहीं है।

उदाहरण 2 प्रश्न हल करें कुल्हाड़ी - 6 \u003d 2a - 3x।

समाधान:यह एक रेखीय समीकरण है कुल्हाड़ी - 6 \u003d 2a - 3x (1)

ax + 3x = 2a +6

के रूप में समीकरण को फिर से लिखना (ए+3)x = 2(ए+3)आइए दो मामलों पर विचार करें:

ए = -3और ए¹ -3.

अगर ए = -3, फिर कोई वास्तविक संख्या एक्ससमीकरण (1) का मूल है। अगर ए¹ -3 , समीकरण (1) का एक ही मूल है एक्स = 2।

उत्तर:पर ए = -3, एक्स आर ; पर ए ¹ -3, एक्स = 2।

उदाहरण 3 पैरामीटर के किस मूल्य पर एसमीकरण की जड़ों के बीच

2x - 4x - ए 2 + 4ए - 4 = 0और भी जड़ें हैं 1 ?

समाधान: प्रश्न हल करें 2x - 4x - ए 2 + 4ए - 4 = 0- रेखीय समीकरण

2 (ए - 2) एक्स \u003d ए 2 - 4ए +4

2(ए - 2) एक्स \u003d (ए - 2) 2

पर ए = 2समीकरण का हल 0x = 0कोई भी संख्या हो, 1 से भी अधिक हो।

पर ए¹ 2 एक्स =
. शर्त से एक्स> 1, वह है
> 1, ए > 4।

उत्तर:पर ए (2) यू (4; ∞)।

उदाहरण 4 . प्रत्येक पैरामीटर मान के लिए एसमीकरण के मूलों की संख्या ज्ञात कीजिए कुल्हाड़ी = 8।

समाधान। कुल्हाड़ी = 8एक रेखीय समीकरण है।

वाई = ए- क्षैतिज रेखाओं का एक परिवार;

वाई = - ग्राफ एक अतिपरवलय है। हम इन कार्यों के रेखांकन का निर्माण करते हैं।

उत्तर: यदि ए = 0, तब समीकरण का कोई हल नहीं है। अगर एक ≠ 0, तो समीकरण का एक हल है।

उदाहरण 5 . ग्राफ़ का उपयोग करके पता करें कि समीकरण की कितनी जड़ें हैं:

|एक्स| = कुल्हाड़ी - 1।

वाई = | एक्स | ,

वाई = कुल्हाड़ी - 1- ग्राफ एक बिंदु से गुजरने वाली एक सीधी रेखा है (0;-1).

हम इन कार्यों के रेखांकन का निर्माण करते हैं।

उत्तर: कब |ए|>1- एक जड़

पर | ए|≤1 समीकरण की कोई जड़ नहीं है।

उदाहरण 6 . असमानता को हल करें कुल्हाड़ी + 4> 2x + ए 2

समाधान : कुल्हाड़ी + 4> 2x + ए 2
(ए - 2) एक्स>ए 2 - 4. तीन मामलों पर विचार करें।

उत्तर। एक्स> ए + 2पर ए > 2; एक्स<а + 2, पर ए< 2; पर ए = 2कोई समाधान नहीं है।

§ 2. द्विघात समीकरण और असमानताएँ

द्विघात समीकरणरूप का एक समीकरण है ओह ² + बी एक्स + सी = 0 , कहाँ एक≠ 0,

ए, बी , साथ - विकल्प।

एक पैरामीटर के साथ द्विघात समीकरणों को हल करने के लिए, आप निम्न सूत्रों का उपयोग करके हल करने के मानक तरीकों का उपयोग कर सकते हैं:

1 ) द्विघात समीकरण का विभेदक: डी = बी ² - 4 एसी , (
²- एसी)

2) द्विघात समीकरण की जड़ों के सूत्र:एक्स 1 =
, एक्स 2 =
,

(एक्स 1,2 =
)

वर्ग असमानताओं को रूप की असमानताएँ कहा जाता है

ए एक्स 2 + बी एक्स + सी > 0,ए एक्स 2 + बी एक्स + सी< 0, (1), (2)

ए एक्स 2 + बी एक्स + सी ≥ 0,ए एक्स 2 + बी एक्स + सी ≤ 0,(3), (4)

असमानता के समाधान का सेट (3) असमानता के समाधान के सेट (1) और समीकरण को मिलाकर प्राप्त किया जाता है , ए एक्स 2 + बी एक्स + सी = 0।असमानता के समाधान का सेट (4) समान रूप से पाया जाता है।

यदि वर्ग त्रिपद का विविक्तकर ए एक्स 2 + बी एक्स + सी शून्य से कम है, तो a > 0 के लिए त्रिपद सभी x के लिए धनात्मक है आर.

यदि वर्ग ट्रिनोमियल की जड़ें हैं (x 1 < х 2 ), तो a> 0 के लिए यह सेट पर सकारात्मक है(-; एक्स 2 )
(एक्स 2; +) और अंतराल पर नकारात्मक

(एक्स 1; एक्स 2 ). यदि एक< 0, то трехчлен положителен на интервале (х 1; एक्स 2 ) और सभी x के लिए ऋणात्मक है (-; एक्स 1 )
(एक्स 2; +).

उदाहरण 1 प्रश्न हल करें ax² - 2 (a - 1) x - 4 \u003d 0.

यह एक द्विघात समीकरण है

समाधान: विशेष अर्थ ए = 0।

पर ए = 0हमें एक रेखीय समीकरण मिलता है 2x - 4 = 0. इसकी एक ही जड़ होती है एक्स = 2।

पर एक ≠ 0।आइए विवेचक को खोजें।

डी \u003d (ए-1)² + 4ए \u003d (ए + 1)²

अगर ए = -1,वह डी = 0 - एक जड़।

स्थानापन्न करके मूल ज्ञात कीजिए ए = -1।

-x² + 4x - 4 \u003d 0,वह है x² -4x + 4 = 0,हम पाते हैं एक्स = 2।

अगर एक ≠ - 1, वह डी >0 . मूल सूत्र के अनुसार, हम प्राप्त करते हैं:एक्स =
;

एक्स 1 = 2, एक्स 2 = -.

उत्तर:पर ए = 0 और ए = -1समीकरण की एक जड़ है एक्स = 2;पर एक ≠ 0 और

ए ≠ - 1 समीकरण के दो मूल होते हैंएक्स 1 = 2, एक्स 2 =-.

उदाहरण 2 दिए गए समीकरण के मूलों की संख्या ज्ञात कीजिए x²-2x-8-ए=0पैरामीटर मानों के आधार पर एक।

समाधान। आइए इस समीकरण को रूप में फिर से लिखें x²-2x-8=एक

वाई \u003d x²-2x-8- ग्राफ एक परवलय है;

वाई = एक- क्षैतिज रेखाओं का परिवार।

आइए कार्यों के ग्राफ बनाएं।

उत्तर: कब ए<-9 , समीकरण का कोई हल नहीं है; जब a=-9, समीकरण का एक हल होता है; पर ए>-9, समीकरण के दो समाधान हैं।

उदाहरण 3 किस पर एअसमानता (ए - 3) एक्स 2 – 2ax + 3a – 6 >0 x के सभी मानों के लिए है?

समाधान। x के सभी मानों के लिए वर्ग त्रिपद धनात्मक होता है यदि

a-3 > 0 और डी<0, т.е. при а, удовлетворяющих системе неравенств

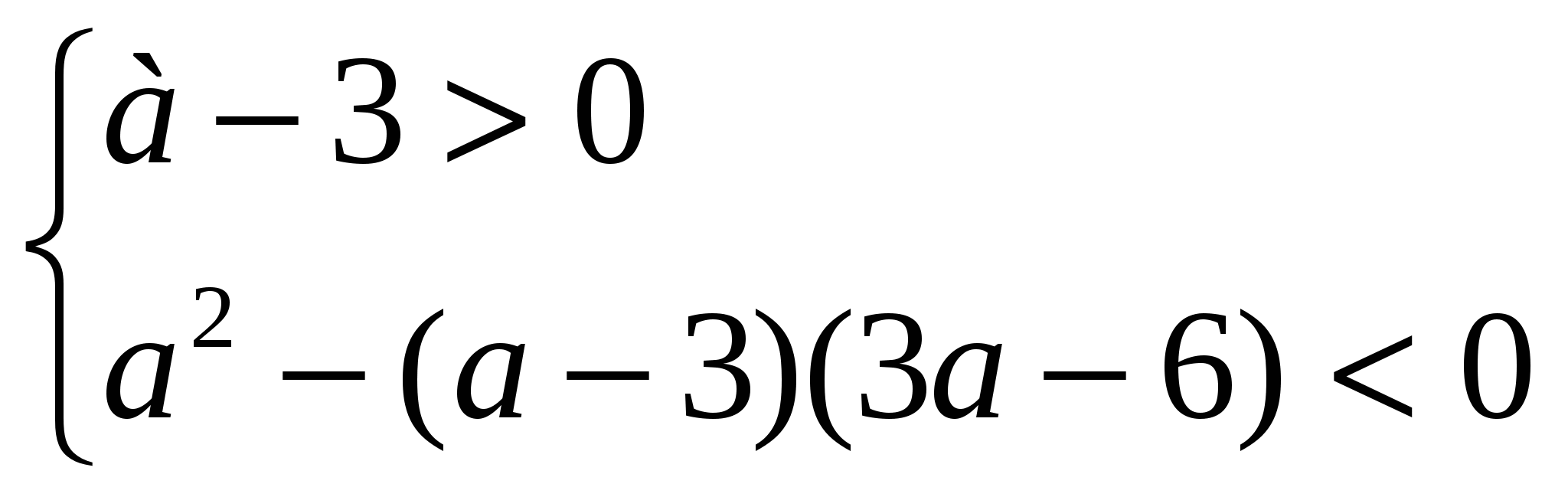
, जहां से यह इस प्रकार हैए > 6 .

उत्तर।ए > 6

§ 3. एक पैरामीटर के साथ भिन्नात्मक-तर्कसंगत समीकरण,

रैखिक में घटाया गया

भिन्नात्मक समीकरणों को हल करने की प्रक्रिया सामान्य योजना के अनुसार की जाती है: भिन्नात्मक को पूर्णांक द्वारा प्रतिस्थापित किया जाता है, समीकरण के दोनों भागों को उसके बाएँ और दाएँ भागों के सामान्य भाजक से गुणा किया जाता है। उसके बाद, बाहरी जड़ों को छोड़कर, पूरे समीकरण को हल किया जाता है, अर्थात, संख्याएँ जो भाजक को शून्य में बदल देती हैं।

पैरामीटर वाले समीकरणों के मामले में, यह समस्या अधिक जटिल है। यहां, बाहरी जड़ों को "समाप्त" करने के लिए, पैरामीटर के मान को खोजने के लिए आवश्यक है जो सामान्य भाजक को शून्य में बदल देता है, अर्थात पैरामीटर के लिए संबंधित समीकरणों को हल करने के लिए।

उदाहरण 1 प्रश्न हल करें
= 0

समाधान: डीजेड: एक्स +2 ≠ 0, एक्स ≠ -2

एक्स - ए \u003d 0, एक्स \u003d ए।

उत्तर:पर ए ≠ - 2, एक्स = ए

पर ए = -2कोई जड़ नहीं है।

उदाहरण 2 . प्रश्न हल करें
-
=
(1)

यह एक आंशिक तर्कसंगत समीकरण है

समाधान:अर्थ ए = 0विशेष है। पर ए = 0समीकरण अपना अर्थ खो देता है और इसलिए इसकी कोई जड़ नहीं होती है। अगर एक ≠ 0,तब परिवर्तनों के बाद समीकरण रूप ले लेगा: x² + 2 (1-ए) एक्स + ए² - 2ए - 3 = 0 (2)- द्विघात समीकरण।

आइए विवेचक को खोजें \u003d (1 - ए)² - (ए² - 2 ए - 3) \u003d 4, समीकरण की जड़ें खोजेंएक्स 1 = ए + 1, एक्स 2 = ए - 3।

समीकरण (1) से समीकरण (2) तक जाने पर, समीकरण (1) की परिभाषा के क्षेत्र का विस्तार हुआ, जिससे बाहरी जड़ें दिखाई दे सकती हैं। इसलिए सत्यापन जरूरी है।

इंतिहान।पाए गए मानों से बाहर करें एक्सजिनमें

x 1 +1=0, x 1 +2=0, x 2 +1=0, x 2 +2=0।

अगर एक्स 1 +1=0, वह है (ए+1) + 1= 0, वह ए = -2।इस प्रकार,

पर ए = -2 , एक्स 1 -

अगर एक्स 1 +2=0, वह है (ए+1)+2=0,वह ए = - 3. इस प्रकार, पर ए \u003d - 3, एक्स 1 - समीकरण की बाहरी जड़। (1)।

अगर एक्स 2 +1=0, वह है (ए - 3) + 1 = 0, वह ए = 2. इस प्रकार, पर ए = 2 एक्स 2 - समीकरण का बाह्य मूल (1).

अगर एक्स 2 +2=0, वह है ( ए - 3) + 2 = 0,वह ए = 1. इस प्रकार, पर ए = 1,

एक्स 2 - समीकरण की बाहरी जड़ (1)।

इसके अनुसार, ए = - 3हम पाते हैं एक्स \u003d - 3 - 3 \u003d -6;

पर ए \u003d - 2 एक्स \u003d -2 – 3= - 5;

पर ए \u003d 1 एक्स \u003d 1 + 1 \u003d 2;

पर ए \u003d 2 एक्स \u003d 2 + 1 \u003d 3।

आप उत्तर लिख सकते हैं।

उत्तर: 1) अगर एक = -3,वह एक्स = -6; 2) अगर ए = -2, वह एक्स = -5; 3) अगर ए = 0, तो कोई जड़ नहीं है; 4) अगर ए = 1, वह एक्स = 2; 5) अगर ए = 2, वह एक्स = 3; 6) अगर a ≠ -3, a ≠ -2, a ≠ 0, a ≠ 1, a ≠ 2, फिर x 1 = ए + 1, एक्स 2 = ए-3।

§4। अपरिमेय समीकरण और असमानताएँ

वे समीकरण तथा असमिकाएँ जिनमें मूल चिह्न के अंतर्गत चर निहित होता है, कहलाते हैं तर्कहीन।

अपरिमेय समीकरणों के समाधान को अपरिमेय से परिमेय समीकरण में परिवर्तित करने के लिए समीकरण के दोनों पक्षों को एक घात में बढ़ाकर या चर को बदलकर कम कर दिया जाता है। जब समीकरण के दोनों पक्षों को एक समान शक्ति तक उठाया जाता है, तो बाहरी जड़ें दिखाई दे सकती हैं। इसलिए, इस पद्धति का उपयोग करते समय, सभी पाए गए जड़ों को मूल समीकरण में प्रतिस्थापन द्वारा जांचा जाना चाहिए, पैरामीटर मानों में परिवर्तन को ध्यान में रखते हुए।

समीकरण टाइप करें
=g (x ) सिस्टम के बराबर है

असमानता f (x) ≥ 0 समीकरण f (x) = g 2 (x) से अनुसरण करती है।

अपरिमेय असमानताओं को हल करते समय, हम निम्नलिखित समकक्ष परिवर्तनों का उपयोग करेंगे:

≤ जी (एक्स)


≥जी (एक्स)

उदाहरण 1 प्रश्न हल करें
= एक्स + 1 (3)

यह एक अपरिमेय समीकरण है

समाधान: अंकगणितीय मूल की परिभाषा के अनुसार, समीकरण (3) निकाय के तुल्य है
.

पर ए = 2सिस्टम के पहले समीकरण का रूप है 0 एक्स = 5यानी इसका कोई समाधान नहीं है।

पर ए≠ 2 एक्स =
. आइए जानें कि किन मूल्यों के लिएए पाया मूल्यएक्स असमानता को संतुष्ट करता हैएक्स ≥ -1:
≥ - 1,
≥ 0,

कहाँ एक ≤या ए> 2।

उत्तर:पर a≤, a > 2 x=
, पर < а ≤ 2 समीकरण का कोई हल नहीं है।

उदाहरण 2 प्रश्न हल करें
= ए (अनुबंध 4)

समाधान। वाई =

वाई = एक्षैतिज रेखाओं का परिवार है।

आइए कार्यों के ग्राफ बनाएं।

उत्तर: पर ए<0 - कोई समाधान नहीं है

पर ए≥ 0 - एक हल।

उदाहरण 3 . आइए असमानता को हल करें(ए+1)
<1.

समाधान। O.D.Z। एक्स ≤ 2. अगर ए+1 ≤0, तब असमानता सभी स्वीकार्य मूल्यों पर लागू होती है एक्स. अगर ए+1>0, वह

(ए+1)
<1.

<

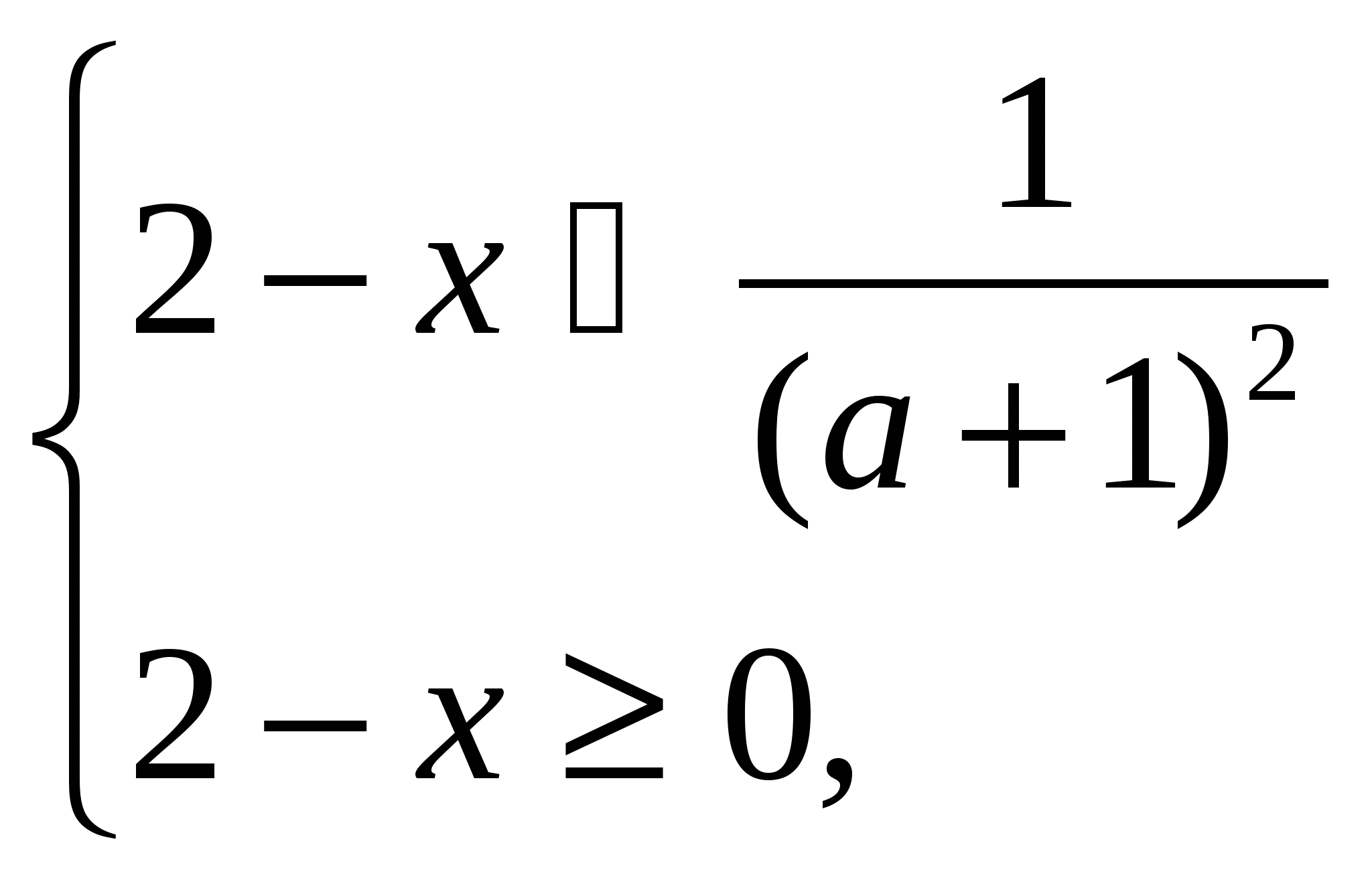
कहाँ एक्स (2-
2

उत्तर। एक्स (- ;2एक पर (-;-1, एक्स (2-
2

पर ए (-1;+).

§ 5. त्रिकोणमितीय समीकरण और असमानताएं।

यहाँ सबसे सरल त्रिकोणमितीय समीकरणों को हल करने के सूत्र दिए गए हैं:

सिंक्स = ए
एक्स = (-1)एन आर्क्सिन ए+πएन, एन जेड, ≤1, (1)

कॉस एक्स = ए
एक्स = ± आर्ककोस ए + 2 πn, एन जेड, ≤1. (2)

अगर >1, तो समीकरण (1) और (2) का कोई हल नहीं है।

तन एक्स = ए
एक्स = आर्कटग ए + πn, एन जेड, ए आर

सीटीजी एक्स = ए
एक्स = आर्कक्टग ए + πn, एन जेड, ए आर

प्रत्येक मानक असमानता के लिए, हम समाधान के सेट का संकेत देते हैं:

1. पाप एक्स> ए
आर्क्सिन ए + 2 एन जेड,

पर ए <-1, एक्स आर ; पर ए ≥ 1, कोई समाधान नहीं है।

2. . पाप एक्स< a
π - आर्क्सिन ए + 2 πnZ,

a≤-1 के लिए, कोई समाधान नहीं हैं; जब एक> 1,एक्स आर

3. ओल एक्स > ए
- arccos ए + 2 पीएन < एक्स < arccos ए + 2 पीएन , एन जेड ,

पर ए<-1, एक्स आर ; पर ए ≥ 1 , कोई उपाय नहीं हैं।

4. कॉस एक्स आर्ककोस ए+ 2 एनजेड,

पर ए≤-1 , कोई समाधान नहीं है; परए > 1, एक्स आर

5. टीजी एक्स> ए, आर्कटग ए + πnZ

6.टीजी एक्स< a, -π/2 + πn Z

उदाहरण 1। पाना ए, जिसके लिए इस समीकरण का हल है:

Cos 2 x + 2(a-2) cosx + a 2 - 4a - 5 \u003d 0।

समाधान।हम समीकरण को रूप में लिखते हैं

साथओएस 2 एक्स + (2 ए -4) cosx +(ए – 5)(ए+1) =0,इसे एक वर्ग के रूप में हल करने पर, हम प्राप्त करते हैं cosx = 5-एऔर cosx = -ए-1।

समीकरण cosx = 5- ए समाधान प्रदान किया है -1≤ 5-ए ≤1
4≤ ए≤ 6, और समीकरण cosx = - एक-1 बशर्ते -1≤ -1-ए ≤ 1
-2 ≤ ए ≤0.

उत्तर। ए -2; 0
4; 6

उदाहरण 2 किस पर बीवहाँ एक ऐसा मौजूद है कि असमानता
+ बी> 0 सभी x ≠ के लिए संतुष्ट हैपीएन , एन जेड .

समाधान।चलो रखो ए= 0. असमानता b >0 पर लागू होती है। आइए अब दिखाते हैं कि कोई भी b ≤0 समस्या की शर्तों को संतुष्ट नहीं करता है। दरअसल, यह x = लगाने के लिए पर्याप्त है π /2, अगर ए <0, и х = - π /2 पर ए ≥0.

उत्तर।बी > 0

§ 6. घातीय समीकरण और असमानताएं

1. समीकरण एच(एक्स) एफ ( एक्स ) = एच(एक्स) जी ( एक्स) पर एच(एक्स) > 0 दो प्रणालियों के संयोजन के बराबर है
और

2. एक विशेष मामले में (एच (एक्स) = ए ) समीकरण एएफ (एक्स) = एजी (एक्स) पर ए> 0, दो प्रणालियों के संयोजन के बराबर है

और

3. समीकरण एएफ (एक्स) = बी , कहाँ ए > 0, ए ≠1, बी> 0, समीकरण के समतुल्य है

f(x)= log a b । हो रहा ए= 1 को अलग से माना जाता है।

सबसे सरल घातीय असमानताओं का समाधान डिग्री संपत्ति पर आधारित है। रूप की असमानताएफ(ए एक्स ) > 0 चर बदलकरटी= ए एक्स असमानताओं की प्रणाली को हल करने के लिए कम कर देता है
और फिर संबंधित सरलतम घातीय असमानताओं के समाधान के लिए।

एक गैर-सख्त असमानता को हल करते समय, सख्त असमानता के समाधान के सेट में संबंधित समीकरण की जड़ों को जोड़ना आवश्यक है। जैसा कि व्यंजक वाले सभी उदाहरणों में समीकरणों को हल करने में होता है ए f (x ), हम मानते हैं ए> 0. प्रकरण ए= 1 को अलग से माना जाता है।

उदाहरण 1 . किस पर एसमीकरण 8 एक्स =
केवल सकारात्मक जड़ें हैं?

समाधान। एक से अधिक आधार वाले एक्सपोनेंशियल फ़ंक्शन की संपत्ति से, हमारे पास x> 0 है
8 एक्स >1

>1

>0, कहा सेए (1,5;4).

उत्तर। ए (1,5;4).

उदाहरण 2 असमानता को हल करें ए 2 ∙2 एक्स > ए

समाधान. तीन मामलों पर विचार करें:

1. ए< 0 . चूँकि असमानता का बायाँ भाग धनात्मक है और दायाँ भाग ऋणात्मक है, असमानता किसी भी x के लिए लागू होती है आर.

2. ए= 0। कोई उपाय नहीं हैं।

3. ए > 0 . ए 2 ∙2 एक्स > ए
2 एक्स >
एक्स> -लॉग 2 ए

उत्तर। एक्स आरपर ए > 0; के लिए कोई समाधान नहीं ए = 0; एक्स (- लकड़ी का लट्ठा 2 ए; +) परए> 0 .

§ 7. लघुगणकीय समीकरण और असमानताएँ

आइए हल करने में प्रयुक्त कुछ तुल्यताओं को प्रस्तुत करें लघुगणकीय समीकरण और असमानताएँ।

1. समीकरण लॉग एफ (एक्स) जी (एक्स) \u003d लॉग एफ (एक्स) एच (एक्स) सिस्टम के बराबर है

विशेष रूप से, अगर ए >0, ए≠1, फिर

लकड़ी का लट्ठा ए जी(एक्स)=लॉग ए ज(एक्स)

2. समीकरण लकड़ी का लट्ठा ए जी (एक्स) = बी
जी (एक्स) =ए बी ( ए >0, एक ≠ 1, जी (एक्स)> 0)।

3. असमानता लकड़ी का लट्ठा एफ ( एक्स ) जी (एक्स) ≤ लकड़ी का लट्ठा एफ ( एक्स ) एच(एक्स) दो प्रणालियों के संयोजन के बराबर है:
और

यदि एक, b संख्याएँ हैं, a >0, a ≠1, तब

लकड़ी का लट्ठा ए एफ (एक्स) ≤ बी

लकड़ी का लट्ठा ए एफ (एक्स)> बी

उदाहरण 1 प्रश्न हल करें

समाधान. आइए ODZ ज्ञात करें: x > 0, x ≠ ए 4 , ए > 0, ए≠ 1. समीकरण को रूपांतरित करें

लकड़ी का लट्ठा एक्स - 2 = 4 - लकड़ी का लट्ठा ए एक्स
लकड़ी का लट्ठा एक्स + लकड़ी का लट्ठा ए एक्स- 6 = 0, जहां से लकड़ी का लट्ठा ए एक्स = - 3

एक्स = ए-3 और लकड़ी का लट्ठा ए एक्स = 2
एक्स = ए 2. हालत एक्स = ए 4
ए – 3 = ए 4 या ए 2 = ए 4 ODZ पर नहीं किया गया।

उत्तर:एक्स = ए-3, एक्स = ए 2 पर ए (0; 1)
(1; ).

उदाहरण 2 . उच्चतम मान ज्ञात कीजिए ए, जिसके लिए समीकरण

2 लकड़ी का लट्ठा -
+ ए = 0 का हल है।

समाधान। चलो बदलो
= टीऔर द्विघात समीकरण 2 प्राप्त करेंटी 2 – टी + ए = 0. हल करने पर हम पाते हैंडी = 1-8 ए . विचार करना डी≥0, 1-8 ए ≥0
ए ≤.

पर ए = द्विघात समीकरण का एक मूल होता हैटी= >0.

उत्तर। ए =

उदाहरण 3 . असमानता को हल करेंलकड़ी का लट्ठा(एक्स 2 – 2 एक्स + ए ) > - 3

समाधान। आइए असमानताओं की प्रणाली को हल करें

वर्ग ट्रिनोमियल्स x की जड़ें 1,2 = 1 ±
उनका 3,4 = 1 ±
.

महत्वपूर्ण पैरामीटर मान: ए= 1 और ए= 9.

मान लीजिए कि X 1 और X 2 पहली और दूसरी असमिकाओं के हल समुच्चय हैं, तब

एक्स 1
एक्स 2 = X मूल असमिका का हल है।

0 पर< ए <1 Х 1 = (- ;1 -
)
(1 +
; +), परए> 1 एक्स 1 = (-;+).

0 पर< ए < 9 Х 2 = (1 -
; 1 +
), परए≥9 Х 2 - कोई समाधान नहीं।

तीन मामलों पर विचार करें:

1. 0< ए ≤1 एक्स = (1 -
;1 -
)
(1 +
;1 +
).

2. 1 < ए < 9 Х = (1 -
;1 +
).

3. ए≥ 9 एक्स - कोई समाधान नहीं।

कार्यों का उपयोग करें

उच्च स्तर C1, C2

उदाहरण 1 सभी मान खोजें आर, जिसके लिए समीकरण

आर ∙ सीटीजी 2x+2sinx+ पी= 3 का कम से कम एक मूल है।

समाधान।चलिए समीकरण बदलते हैं

आर ∙ (
-1)+2sinx+ पी\u003d 3, sinx \u003d टी, टी
, टी 0.

- पी+ 2t + पी = 3, + 2t = 3, 3 -2t = , 3t2 - 2t3 = पी .

होने देना एफ(वाई) = 3 टी 2 – 2 टी 3 . आइए फ़ंक्शन मानों का सेट ढूंढेंएफ(एक्स) पर


. पर / = 6 टी – 6 टी 2 , 6 टी - 6 टी 2 = 0, टी 1 =0, टी 2 = 1. एफ(-1) = 5, एफ(1) = 1.

पर टी
, इ(एफ) =
,

पर टी
, इ(एफ) =
, तभी टी


, इ(एफ) =
.

समीकरण 3 के लिएटी 2 – 2 टी 3 = पी (इसलिए दिए गए) में कम से कम एक जड़ आवश्यक और पर्याप्त थीपी इ(एफ), वह है पी
.

उत्तर।
.

उदाहरण 2

पैरामीटर के किस मूल्य परएसमीकरण लकड़ी का लट्ठा
(4 एक्स 2 – 4 ए + ए 2 +7) = 2 का ठीक एक मूल है?

समाधान।आइए समीकरण को समकक्ष में बदलें:

4एक्स 2 - 4 ए + ए 2 +7 \u003d (x 2 + 2) 2।

ध्यान दें कि यदि एक निश्चित संख्या x परिणामी समीकरण का मूल है, तो संख्या - x भी इस समीकरण का मूल है। शर्त के अनुसार, यह संभव नहीं है, इसलिए एकमात्र रूट संख्या 0 है।

पता लगाते हैं ए.

4∙ 0 2 - 4ए + ए 2 +7 = (0 2 + 2) 2 ,

ए 2 - 4ए +7 = 4, ए 2 - 4ए +3 = 0, ए 1 = 1, ए 2 = 3.

इंतिहान।

1) ए 1 = 1। तब समीकरण का रूप है:लकड़ी का लट्ठा
(4 एक्स 2 +4) =2। हम इसे हल करते हैं

4x 2 + 4 \u003d (x 2 + 2) 2, 4x 2 + 4 \u003d x 4 + 4x 2 + 4, x 4 \u003d 0, x \u003d 0 एकमात्र जड़ है।

2) ए 2 = 3. समीकरण ऐसा दिखता है:लकड़ी का लट्ठा
(4 एक्स 2 +4) =2
x = 0 ही एक मूल है।

उत्तर। 1; 3

उच्च स्तर C4, C5

उदाहरण 3 सभी मान खोजें आर,जिसके तहत समीकरण

एक्स 2 - ( आर+ 3)x + 1= 0 में पूर्णांक जड़ें हैं और ये जड़ें असमानता के समाधान हैं: x 3 - 7 आरएक्स 2 + 2x 2 - 14 आरएक्स - 3x +21 आर ≤ 0.

समाधान। चलो एक्स 1, एक्स 2 समीकरण x के पूर्णांक मूल हैं 2 – (आर + 3)x + 1= 0। फिर, वीटा सूत्र द्वारा, x 1 + एक्स 2 = आर + 3, एक्स 1 ∙ एक्स 2 = 1. दो पूर्णांक x का गुणनफल 1 , एक्स 2 केवल दो स्थितियों में एक के बराबर हो सकता है: x 1 = एक्स 2 = 1 या एक्स 1 = एक्स 2 = - 1. यदि x 1 = एक्स 2 = 1, फिरआर + 3 = 1+1 = 2
आर = - 1; अगर एक्स 1 = एक्स 2 = - 1, तबआर + 3 = - 1 – 1 = - 2
आर = - 5. जाँच कीजिए कि क्या समीकरण x के मूल हैं 2 – (आर + 3)x + 1= 0 इस असमानता के समाधान द्वारा वर्णित मामलों में। अवसर के लिएआर = - 1, एक्स 1 = एक्स 2 = 1 हमारे पास है

1 3 - 7 ∙ (- 1) ∙ 1 2 +2 ∙ 1 2 - 14 ∙ (- 1) ∙ 1 - 3 ∙ 1 + 21 ∙ (- 1) = 0 ≤ 0 - सत्य; मामले के लिए आर\u003d - 5, x 1 \u003d x 2 \u003d - 1 हमारे पास है (- 1) 3 - 7 ∙ (- 5) ∙ (-1) 2 + 2 ∙ (-1) 2 - 14 ∙ (-5) × (- 1 ) – 3 ∙ (- 1) + 21 ∙ (-5) = - 136 ≤ 0 सही है। तो, समस्या की स्थिति ही संतुष्ट है आर= - 1 और आर = - 5.

उत्तर।आर 1 = - 1 और आर 2 = - 5.

उदाहरण 4 सभी सकारात्मक पैरामीटर मान खोजें ए, जिसके लिए नंबर 1 फ़ंक्शन के डोमेन से संबंधित है

पर = (ए
- ए
).

इस पाठ में, हम पैरामीटर के साथ असमानताओं को हल करने के लिए एल्गोरिथम का अध्ययन करेंगे और सीखेंगे कि इस प्रकार के कार्यों को हल करते समय इसे कैसे लागू किया जाए।

परिभाषा एक.

एक पैरामीटर के साथ असमानता को हल करने का मतलब है, पैरामीटर के प्रत्येक मान के लिए, इस असमानता के सभी समाधानों का सेट ढूंढना या यह साबित करना कि कोई समाधान नहीं है।

रैखिक असमानताओं पर विचार करें।

परिभाषा दो.

फॉर्म की असमानताएं एक्स प्लस शून्य से अधिक, शून्य से अधिक या उसके बराबर, शून्य से कम, शून्य से कम या बराबर, जहां एऔर b वास्तविक संख्याएँ हैं, एक्स- एक चर कहा जाता है पहली डिग्री की असमानताएं (रैखिक असमानताएं)।

एक पैरामीटर के साथ एक रैखिक असमानता को हल करने के लिए एक एल्गोरिदम, उदाहरण के लिए, असमानता एक्स प्लस बी शून्य से अधिक है, जहां एऔर b वास्तविक संख्याएँ हैं, एक्स- चर। निम्नलिखित मामलों पर विचार करें:

पहला मामला:एशून्य से बड़ा है, तो x माइनस ba से विभाजित a से बड़ा है।

नतीजतन, असमानता के समाधान का सेट एक खुली संख्यात्मक किरण है जो माइनस से एक से अधिक अनंत तक विभाजित होती है।

दूसरा मामला:एशून्य से कम, तो x माइनस ba से विभाजित a से कम है

और, परिणामस्वरूप, असमानता के समाधान का सेट एक खुली संख्यात्मक किरण है जो माइनस इनफिनिटी से माइनस तक एक से विभाजित होती है।

तीसरा मामला: एशून्य के बराबर है, तो असमानता रूप लेगी: शून्य गुणा एक्स प्लस बी शून्य से अधिक है और के लिए बीएईशून्य से अधिक, कोई वास्तविक संख्या असमानता का समाधान है, और कब बीएईशून्य से कम या उसके बराबर, असमानता का कोई हल नहीं है।

शेष असमानताओं को इसी तरह हल किया जाता है।

उदाहरणों पर विचार करें।

अभ्यास 1

असमानता को हल करें और x एक से कम या उसके बराबर है।

समाधान

संकेत के आधार पर एतीन मामलों पर विचार करें।

पहला मामला: अगर एशून्य से अधिक, तो x एक से विभाजित एक से कम या उसके बराबर है;

दूसरा मामला: अगर एशून्य से कम, तो x एक से विभाजित एक से अधिक या उसके बराबर है;

तीसरा मामला: अगर एशून्य के बराबर है, तो असमानता रूप लेगी: शून्य गुणा x एक से कम या बराबर है और इसलिए, कोई भी वास्तविक संख्या मूल असमानता का समाधान है।

इस प्रकार, यदि एशून्य से अधिक है, तो x माइनस इनफिनिटी से एक से विभाजित एक किरण से संबंधित है।

अगर ए एशून्य के बराबर है,

वह एक्स

उत्तर: अगर एशून्य से अधिक है, तो x माइनस इनफिनिटी से किरण से संबंधित है जो एक से विभाजित एकता है;

अगर एशून्य से कम है, तो x किरण से संबंधित है एक से विभाजित एक से अधिक अनंत तक, और यदि एशून्य के बराबर है,

वह एक्स x वास्तविक संख्याओं के समुच्चय से संबंधित है।

कार्य 2

असमानता mod x ऋण दो को a और एक के बीच के अंतर के ऋणात्मक वर्ग से अधिक हल करें।

समाधान

ध्यान दें कि सापेक्ष x ऋण दो किसी भी वास्तविक के लिए शून्य से अधिक या उसके बराबर है एक्सऔर पैरामीटर के किसी भी मान के लिए एक और एकता के बीच के अंतर का वर्ग शून्य से कम या उसके बराबर है ए. इसलिए, अगर एएक के बराबर है, तो कोई भी एक्स- दो के अलावा एक वास्तविक संख्या असमानता का समाधान है, और यदि एएक के बराबर नहीं है, तो कोई भी वास्तविक संख्या असमिका का एक हल है।

उत्तर: अगर एएक के बराबर है, तो x माइनस इनफिनिटी से दो और दो से प्लस इनफिनिटी तक दो खुली संख्यात्मक किरणों के मिलन से संबंधित है,

और अगर एमाइनस इनफिनिटी से एक और एक से प्लस इनफिनिटी तक दो खुली संख्यात्मक किरणों के मिलन से संबंधित है एक्सवास्तविक संख्याओं के समुच्चय के अंतर्गत आता है।

कार्य 3

असमानता तीन को चार ए और एक्स के अंतर से दो ए एक्स प्लस तीन से कम करके हल करें।

समाधान

इस असमानता के प्राथमिक परिवर्तनों के बाद, हमें असमानता मिलती है: दो a और तीन के योग का x गुना, चार a और एक के अंतर के तीन गुना से अधिक है।

पहला मामला: यदि दो और तीन शून्य से अधिक है, अर्थात एऋण तीन सेकंड से अधिक है, तो x एक भिन्न से बड़ा है, जिसका अंश चार a और एक के अंतर का तीन गुना है, और भाजक दो a धन तीन है।

दूसरा मामला: यदि दो और तीन शून्य से कम है, अर्थात एमाइनस तीन सेकंड से कम, तो x एक अंश से कम है, जिसका अंश चार a और एक के अंतर का तीन गुना है, और भाजक दो और तीन है।

तीसरा मामला: यदि दो और तीन का योग शून्य के बराबर है, अर्थात एमाइनस तीन सेकंड के बराबर,

कोई भी वास्तविक संख्या मूल असमानता का समाधान है।

इसलिए, यदि a माइनस तीन सेकंड से प्लस इनफिनिटी तक एक ओपन नंबर रे से संबंधित है, तो x

एक अंश से एक खुली संख्यात्मक किरण के अंतर्गत आता है, जिसका अंश चार ए और एक के अंतर का तीन गुना है, और भाजक दो एक प्लस तीन है, प्लस अनंत तक।

यदि a माइनस इनफिनिटी से माइनस तीन सेकंड तक एक ओपन न्यूमेरिकल किरण से संबंधित है, तो x माइनस इनफिनिटी से एक ओपन न्यूमेरिकल किरण से संबंधित है, जिसका अंश चार और एक के अंतर का तीन गुना है, और हर दो प्लस प्लस है तीन;

अगर एफिर माइनस तीन सेकंड के बराबर होता है एक्सवास्तविक संख्याओं के समुच्चय के अंतर्गत आता है।

उत्तर: यदि a माइनस तीन सेकंड से प्लस इनफिनिटी तक एक खुली संख्या वाली किरण से संबंधित है, तो x

एक अंश से एक खुली संख्यात्मक किरण के अंतर्गत आता है, जिसका अंश चार और एक के अंतर का तीन गुना है, और भाजक दो एक प्लस तीन से प्लस अनंत है;

यदि a माइनस इनफिनिटी से माइनस तीन सेकंड तक एक ओपन न्यूमेरिकल किरण से संबंधित है, तो x माइनस इनफिनिटी से एक ओपन न्यूमेरिकल किरण से संबंधित है, जिसका अंश चार और एक के अंतर का तीन गुना है, और हर दो प्लस है तीन;

अगर एफिर माइनस तीन सेकंड के बराबर होता है एक्सवास्तविक संख्याओं के समुच्चय के अंतर्गत आता है।

कार्य 4

सभी मान्य पैरामीटर मानों के लिए एअसमानता को हल करें x माइनस ए प्लस का वर्गमूल दो ए माइनस x प्लस वर्गमूल का माइनस एक प्लस तीन का वर्गमूल घटा शून्य से बड़ा।

समाधान

पैरामीटर का डोमेन खोजें ए. यह असमानताओं की एक प्रणाली द्वारा निर्धारित किया जाता है, जिसे हल करने से हम पाते हैं कि a एक से तीन तक के खंड से संबंधित है।

यह असमानता असमानताओं की एक प्रणाली के बराबर है, जिसे हल करने पर हमें पता चलता है कि x, a से दो a तक के खंड से संबंधित है।

यदि a एक से तीन तक के खंड से संबंधित है, तो मूल असमानता का समाधान a से दो a तक का खंड है।

उत्तर: यदि a एक से तीन तक के खंड से संबंधित है, तो x, a से दो a तक के खंड से संबंधित है।

कार्य 5

सब ढूँढ़ो एजिसके तहत असमानता है

एक्स का वर्गमूल माइनस एक्स माइनस टू प्लस एक अंश का वर्गमूल जिसका अंश दो माइनस एक्स है और जिसका हर एक्स प्लस चार से अधिक या एक एक्स प्लस दो माइनस अंश का वर्गमूल है जिसका अंश एक्स प्लस वन है a का हर पाँच है माइनस x का कोई हल नहीं है।

समाधान

पहला। आइए हम इस असमानता की परिभाषा के डोमेन की गणना करें। यह असमानताओं की एक प्रणाली द्वारा निर्धारित किया जाता है, जिसका समाधान दो संख्याएँ हैं: x बराबर माइनस एक और x बराबर दो।

दूसरा। आइए हम a के वे सभी मान ज्ञात करें जिनके लिए इस असमानता का समाधान है। ऐसा करने के लिए, हम सब कुछ पा लेंगे ए, जिसके लिए x बराबर ऋण एक और x बराबर दो - यह इस असमानता का समाधान है। दो प्रणालियों के सेट पर विचार करें और हल करें। समाधान दो संख्यात्मक किरणों को माइनस इनफिनिटी से माइनस एक सेकंड और एक से प्लस इनफिनिटी तक संयोजित करना है।

इसलिए, इस असमानता का एक समाधान है यदि a माइनस से दो संख्यात्मक किरणों के मिलन से संबंधित है

अनंत से ऋण एक सेकंड, और एक से प्लस अनंत तक।

तीसरा। इसलिए, इस असमानता का कोई समाधान नहीं है यदि a अंतराल से एक सेकंड से एक तक के अंतराल से संबंधित है।

उत्तर: असमानता का कोई समाधान नहीं है यदि a ऋणात्मक एक सेकंड से एक के अंतराल से संबंधित है।